いろいろ 正多角形 外角 227768

正多角形の意味を用いて作図できることを、外角を利用したプログラミングを通して確認させるとともに、人にとっては難しくともコンピュータであれば容易にできることがあることに気付かせる。 詳細 No24 対称な図形 #B領域 #Scratch #小学校向け算数指導多角形の外角の和 多角形の外角の和は理屈抜きに覚えておきましょう。 正多角形でも普通の多角形でも 外角の和はいつも\(\,360°\,\) です。 多角形の外角とは多角形の頂点の外側の角度のことです。 多角形の内部の一つひとつの角を内角、内角の補角を 辺の長さがみな等しく、角の大きさもみな等しい形を正多角形という。 The sum of the interior and exterior angles of one angle in a polygon is 180 degrees 多角形の1つの角の内角と外角の和は180°です。

正多角形の1つの内角 外角を求める方法を問題解説 数スタ

正多角形 外角

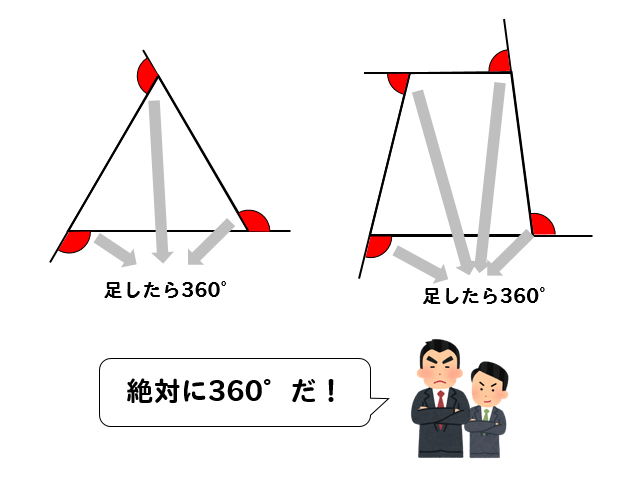
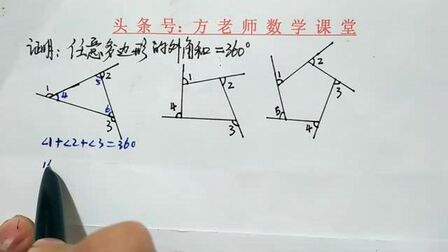
正多角形 外角-これは多角形の外角の和の研究です。 多角形の内角の和は変化しますが、外角の和は一定です。 つまり、内角の和の公式よりも、外角の和の方が本質的だということです。 それを直観的に証明してみましょう。 そして、このことから、外角から正多角形を作ることができます。この性質は多角形、正多角形に関係なく どんなやつでも全部合わせたら360°になります。 では、このことを使って考えると 正多角形の外角1つ分の大きさは $$\LARGE{360 \div (角の数)}$$ をすることによって求めることができます。 正三角形の場合

正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊

さんは，多角形の外角の和が360°であることをも とに，正多角形の1つの外角の大きさについて調べています。 涼太さんは，まず正五角形の1つの外角の大きさを次のように求め ました。 正多角形の外角の大きさはどれも 等しいから，正五角形の1つの外角正多角形の内角と外角の大きさ 具体例で学ぶ数学 > 図形 > 正多角形の内角と外角の大きさ 最終更新日 正多角形の内角の大きさは、頂点の数を n とすれば、 180 ( n − 2) n という公式で計算できます。 正多角形の外角の大きさは、頂点の数を n と 多角形の外角の求め方を5分でサクッと理解！ 外角ってなんですか？ 外角の和とか言われても、意味わからんし というわけで、今回の記事では 「多角形の外角の和、正多角形の1つ分の外角は？ 」 について解説していきます。 5分で理解できるように

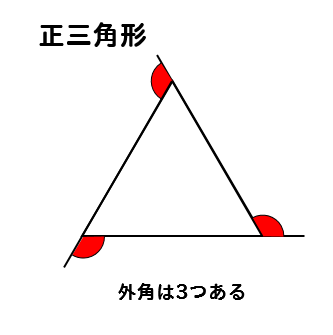
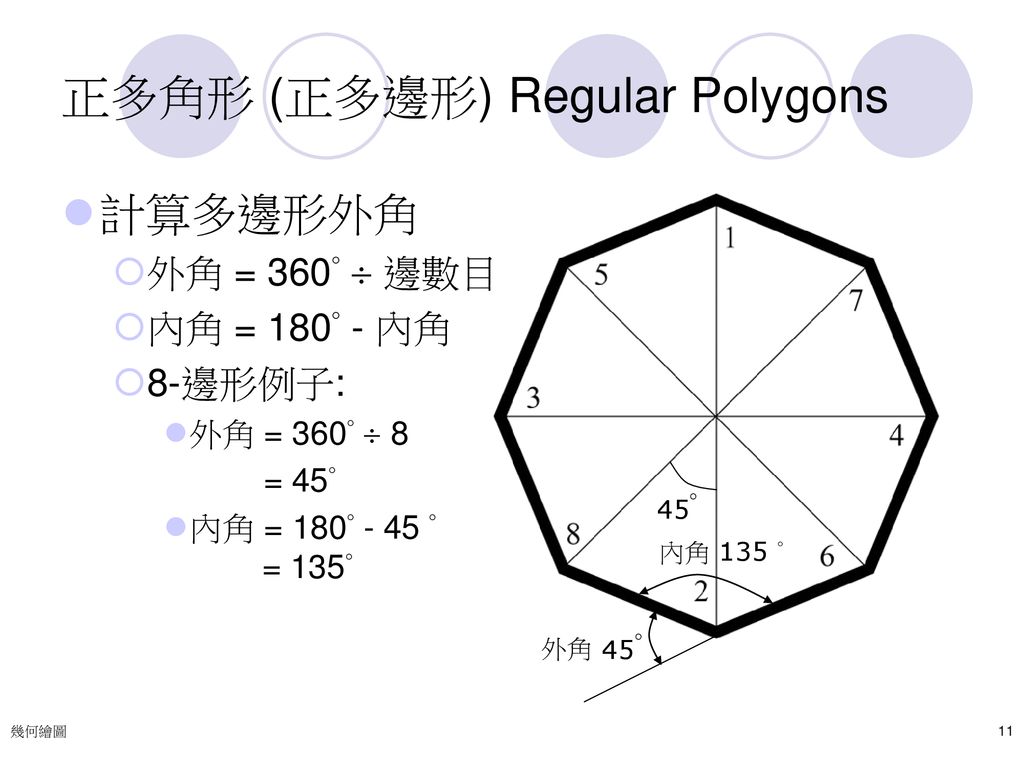
 正多角形の外角の大きさ がわからない・・・・・ そんなときは公式をつかえば一発。 正n角形の外角の1つの大きさは、 360°/n になるんだ。 たとえば、正五角形の外角を求めてみよう。 公式のnに「5」を代入してやればいいから、 360°/ n = 360°/ 5多角形の外角の和は、$\textcolor{blue}{360°}$ となります。 何角形であっても同じ $\textcolor{blue}{360°}$ です。 正三角形の場合を考えてみると、正三角形の $1$ つの内角は $60°$ なので、$1$ つの外角は、$180°60°=\textcolor{blue}{1°}$ となります。 株式会社ベネッセコーポレーションのプログラミング教育の取り組みや、プログラミング教育に関する国内外のニュースや事例を紹介するWebページです。 小5算数 内角の大きさを求めて正多角形を作図しよう について紹介します。

カテゴリ一覧 他の勉強がしたい方はこちら 構造力学の基礎5角形の内角の和は 180°×3=540° すべての辺の長さが等しく,すべての内角の大きさが等しい多角形を 正多角形 という • 多角形の外角の和は 360° 正多角形のすべての内角の大きさは等しく,すべての外角の大きさは等しい 180°× (n−2) 多角形（四角形・五角形・六角形・・・）の内角の和の公式＆問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されま

正多角形の1つの内角 外角を求める方法を問題解説 数スタ

多角形の内角の和 外角の和の公式 数学fun

 (2) 正多角形であるとき、\(1\) つの外角の大きさを求めよ。 (3) 対角線の総数を求めよ。 問われ方が違うだけで、公式を上手く利用すると簡単に解ける問題ですよ。三角形の内角と外角 $ ABC$ において，$\angle A，\angle B，\angle C$ を，$ ABC$ の内角といいます． また，下図の $\angle ACD$ や $\angle BCE$ のように，一つの辺とその隣の辺の延長がつくる角を，外角といいます． さて，三角形の内角と外角について，次の重要な事実が成り立ちます．★無料の中学メルマガ講座★毎週、問題と動画講義をお届け！ 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料

正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊

内角の和 180 N 2 外角の和 360 教遊者

四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^ どうですか？ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで！L02/03正多角形の1つの内角/外角 p1 l041つの内角→正多角形 p2 l05対頂角 p3 l06/07平行線の同位角/錯角 p4 l08平行線の間の角 p4 l09二等分線と角 p5 l10ブーメラン型 p5 l11三角形の合同条件 p6～7練習13 下の図のように大きさも形も同じ二等辺三角形をいくつも使って正多角形を作ります。これについて後の問いに答えなさい。 (1) この正多角形の名前を答えよ。 (2) 図のxの角度を求めよ。 (3) この正多角形の対角線の本数は何本か。

一个多边形的每一个外角都等于30 这个多边形的边数是 它的内角和是 度 初中 数学试题 多边形的内角和和外角和考点 好技网

多边形的内角和与外角和 平行四边形ppt 第2课时 第一ppt

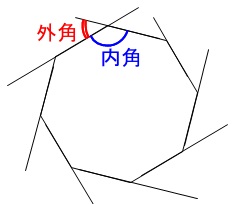
対頂角・平行線と角／三角形と角／二等辺三角形・正三角形／平行四辺形と角／ 多角形の内角の和・外角の和 ／多角形の角：応用／FdData 入試製品版のご案内 FdData 入試ホームページ掲載のpdf ファイル(サンプル)一覧「正多角形」の意味や性質を理解する。 円の中心の周りの角を等分して正多角形をかく方法を理解する。 円の半径の長さを使って正六角形を作図し，正多角形と円の関係について理解を深 める。 （本時各内角には2つの外角があるが,外角の大きさというときには，図3に示すようにそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° になる n角形の

正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

正多边形内角和多边形内角和公式推导方法 尚书坊

正多角形（せいたかっけい、せいたかくけい、regular polygon）とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに 正三角形の1つの内角は60°、外角は1°なので、 外角の和は1°×3＝360° 「あっ、そうそうそうそう、外角の和は360°だったね～」 と思い出そう！！ 多角形の外角の和を忘れたら、正三角形で検証せよ！！ 問題 図に示された角度は、全て三角形の外角だね 正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる！ 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、

正五边形abcde中 你会求 m的度数吗 陕西中考数学真题 多边形的内角和公式 外角和公式 哔哩哔哩 Bilibili

五边形有几个外角正五边形外角和多少度 天奇生活

正多角形の1つの内角・外角を求める方法を問題解説！ 図形と証明 正三角形の角度正方形、ひし形との融合問題を解説！三角形の内角の和は何度か。 x角形の内角の和は何度か。 十角形の内角の和は何度か。 正八角形の一つの内角は何度か。 次の問いに答えよ。 二十角形の内角の和は何度か。 十八角形の内角の和は何度か。 内角の和が 7°になるのは何角形か。

正多边形内角和多边形内角和公式推导方法 尚书坊

正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊

多边形的角 禾教 初中数学互动课堂

已知一个正多边形的每个外角等于则这个正多边形是 X题卡

多邊形外角和多邊形的內角公式和多邊形外角和的簡單證明方法 Yihbk

五邊形外角和外角 Retdy

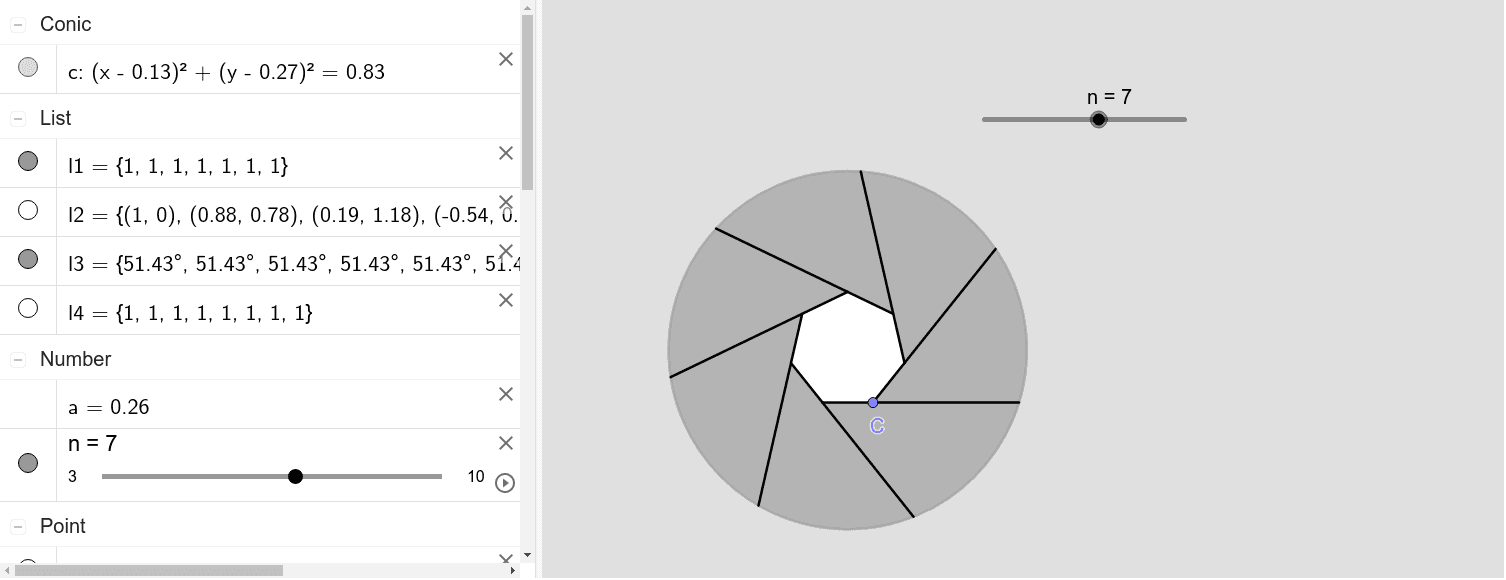
光圈与正多边形外角和 Geogebra

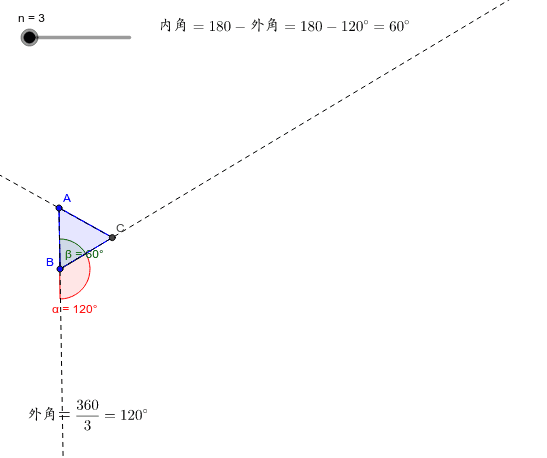
正多角形の外角と内角 Geogebra

1

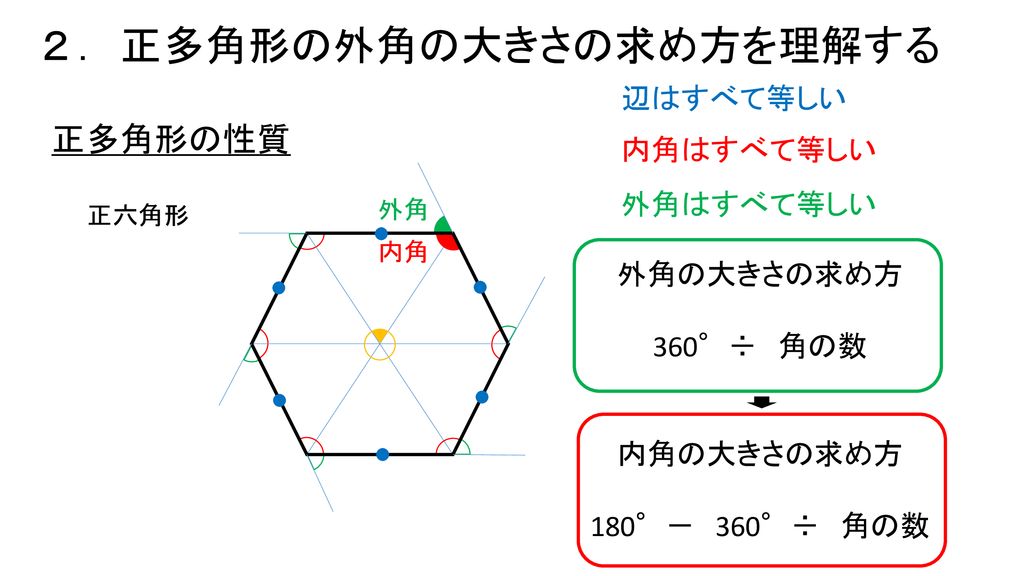
正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download

若一个多边形的内角和等于其外角和的2倍则它是边形 初中数学

正多邊形的一些基本概念 知乎

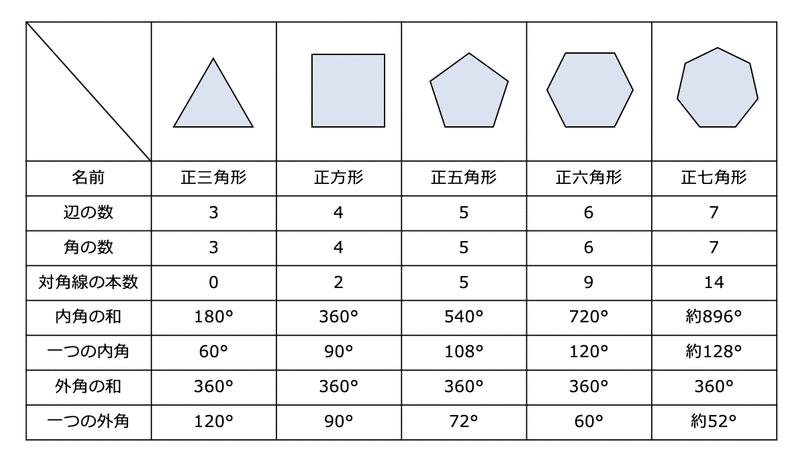
実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note

多边形的内角和与外角和 Ppt课件 第一ppt

正多邊形的結構特點及特性 每日頭條

高中數學知識點 多邊形外角和等於360 動畫版 每日頭條

若 个多边形的内角和等于它的外角和的两倍则这个多边形的边数为 X题卡

正多边形 属性

一个多边形的每一个外角都等于30 这个多边形的边数是 它的内角和是 度 初中 数学试题 多边形的内角和和外角和考点 好技网

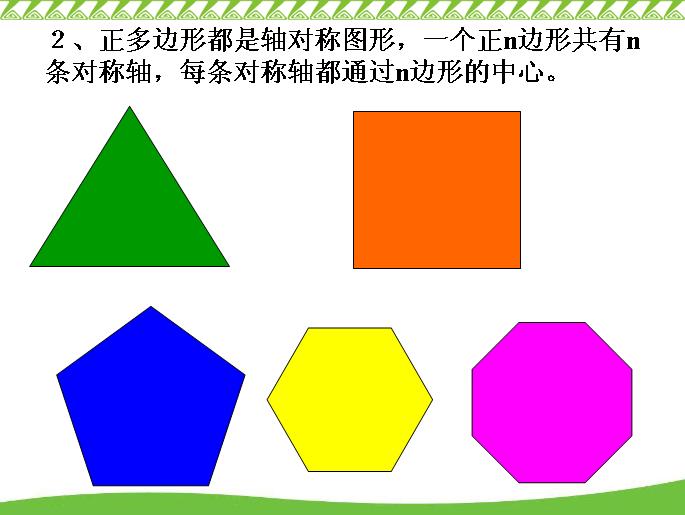
正多邊形 定義 相關概念 外接圓 內切圓 內角 外角 中心角 面積 對稱軸 鑲嵌規 中文百科全書

如何计算多边形的外角之和 数学 21

正星形多角形 快懂百科

人教版九年级上数学 24 3正多边形和圆 练习题 含答案 七七文库www 77wenku Com

多边形外角和计算公式 西瓜视频搜索

多边形的内角和与外角和 简书

内角の和が2340度である正多角形の一つの外角の大きさを求める問題の答えが2 Clearnote

正多角形の内角と外角の大きさ 具体例で学ぶ数学

正多边形外角和公式 搜狗搜索

数学 中2 51 多角形の内角と外角の和 基本編 Youtube

1

多边形内角和公式 万图壁纸网

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

09多边形的外角和平行四边形初中数学初二 Youtube

八边形 维基百科 自由的百科全书

多边形的内角和与外角和题型总结

正多角形の内角と外角の大きさ 具体例で学ぶ数学

正多角形の1つの内角 外角を求める方法を問題解説 数スタ

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

正多边形外角与边数的关系 搜狗搜索

初中几何 一个正多边形的每个外角为60 这个正多边形的内角和是多少度 海燕数学 哔哩哔哩 Bilibili

一个多边形的每一个外角都等于45 则这个多边形的内 初中一年级下学期数学

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

1

正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より

多角形の内角の和 外角の和の公式 数学fun

正多边形外角度数公式 扒拉扒拉

内角正多边形外角定理png图片素材免费下载 图片编号 Png素材网

多边形内角和定理 快懂百科

正多边形外角和公式 搜狗搜索

上6 角形五角形角度 シモネタ

初中数学 圆的性质 正多边形和圆 多边形内 外 角和 1 2 壹读

正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊

小学校5年 算数 正多角形の角の大きさ Youtube

中考重头戏 多边形到圆 极致到完美 每日头条

ひとつの外角が40度の正多角形は正何角形かどう求められますか 教えてください Clearnote

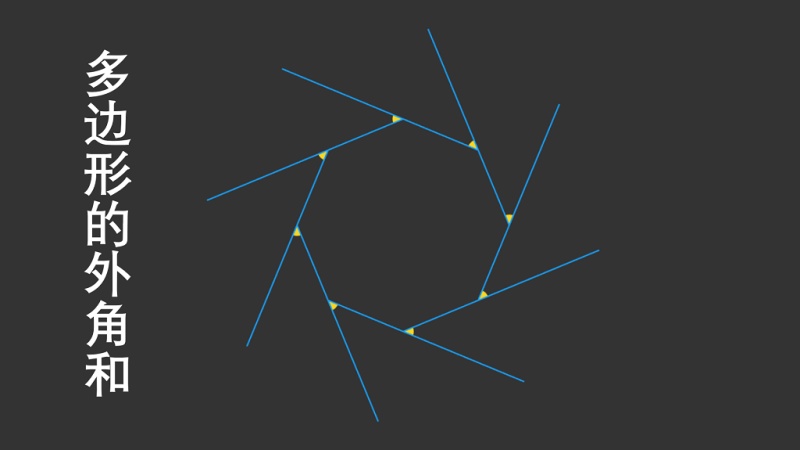
多边形的外角和 火花学院

無料 中２数学 基本解説 解答プリント 223 図形３ 多角形の角

五边形内角和是多少 Abc攻略网

1

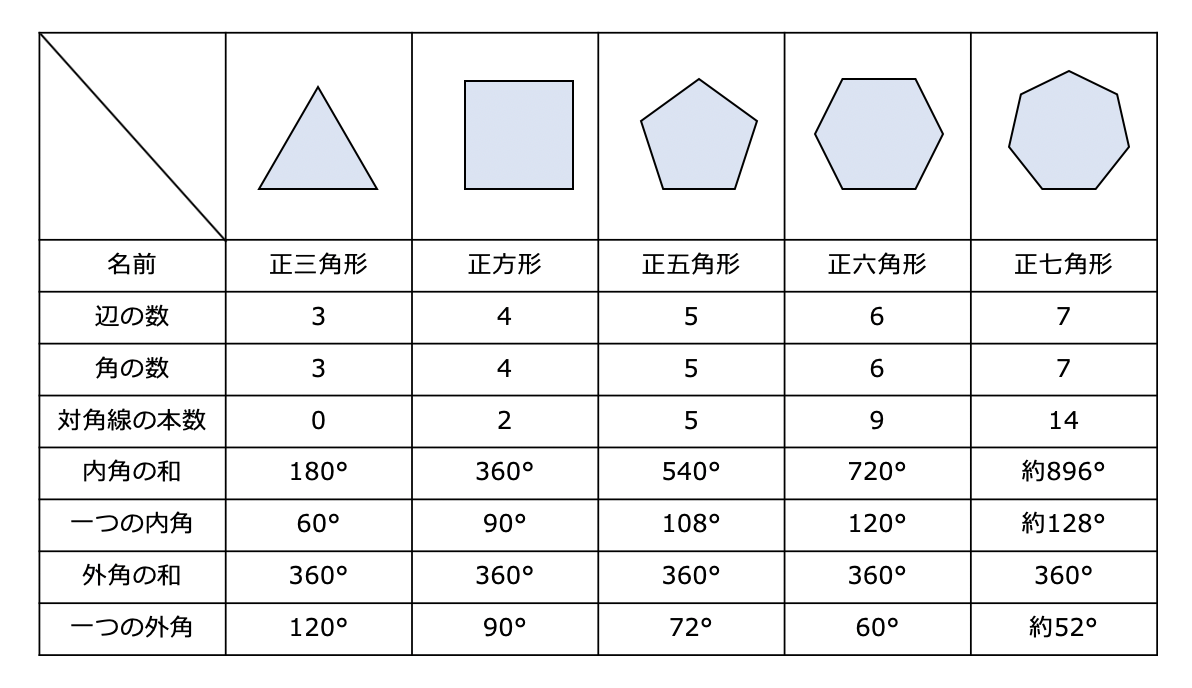
多角形内角和

1つの内角の大きさが 1つの外角の大きさの5倍に等しい正多角形は正何角形です Clearnote

外角是36度是正几边形 西瓜视频搜索

正多角形の1つの内角 外角を求める方法を問題解説 数スタ

正五边形的外角和等于多少度 初三网

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

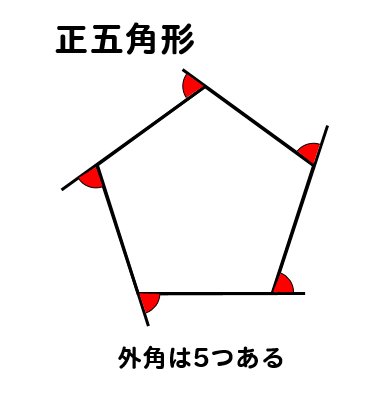
正多角形の1つの内角 外角を求める方法を問題解説 数スタ

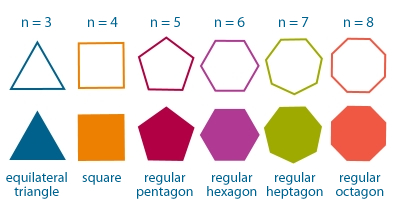
正多邊形的一些基本概念 知乎

N边形的外角的定义 正多边形的外角定义 定义形式网

正多边形外角和公式 初三网

初二数学 一个正多边形内角和为1080 则每个外角度数为多少 哔哩哔哩 つロ干杯 Bilibili

多边形的内角和与外角和 平行四边形ppt 第2课时 第一ppt

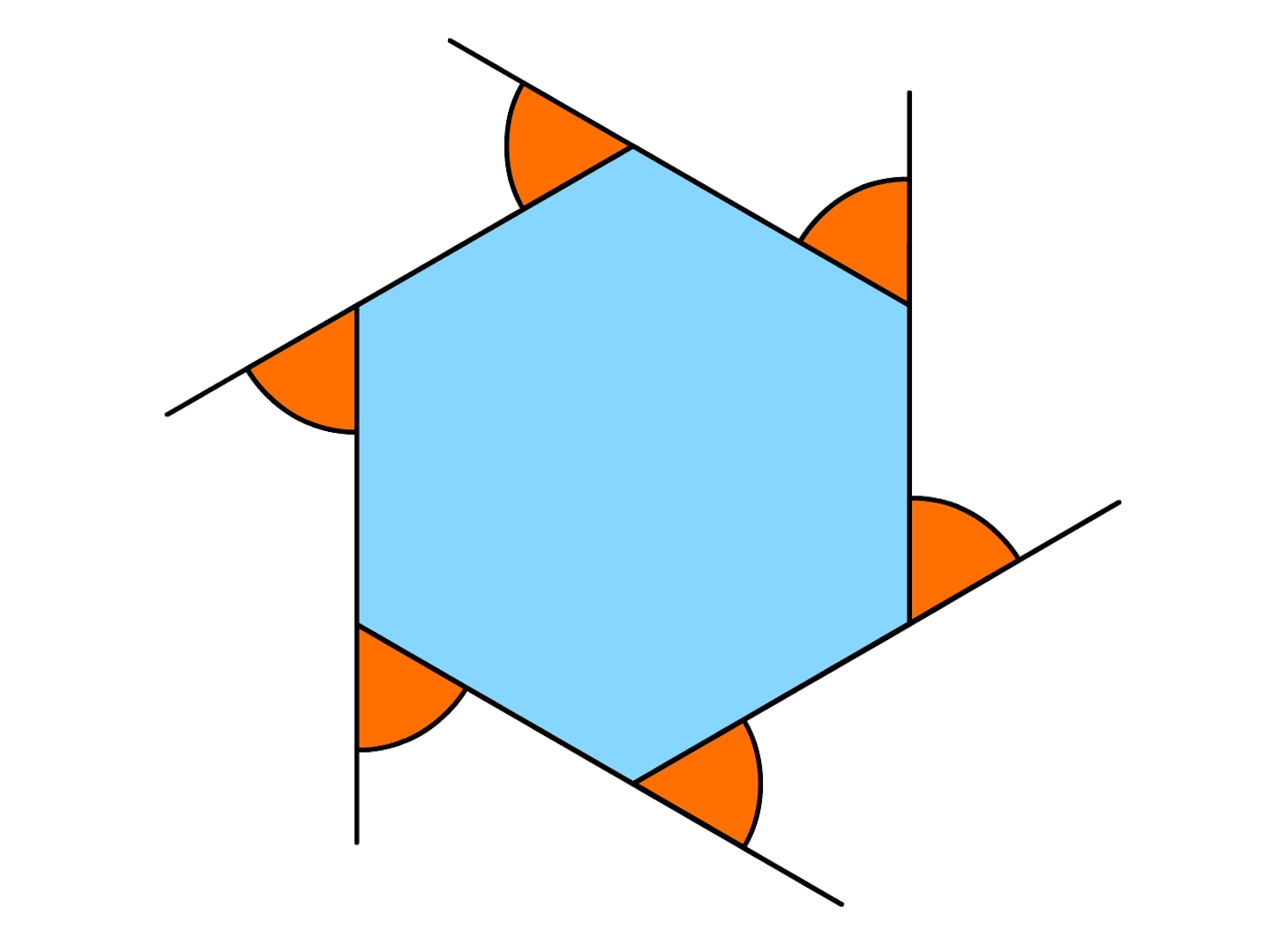
2年 多角形の外角 数学イメージ動画集 大日本図書

70以上8 角形角度 シモネタ

多边形的内角

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

正多邊形的內角與外角 Live 多媒體數學觀念典online

內角和外角 维基百科 自由的百科全书

觀念 N 邊形外角和定理 數學 均一教育平台

多边形的外角和 火花学院

正多角形の1つの内角 外角を求める方法を問題解説 数スタ

正多邊形內角正多邊形的一些基本概念 Mswju

01 004 基础数学之平面几何知识点精讲汇总 多边形 简书

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

多角形の内角の和の公式と外角の和を利用した角度の求め方

正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊

正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊

多边形的内角和与外角和题型总结

多边形的内角和与外角和题型总结

正多边形内角 正多边形内角度数知道正多边形的内角度数怎么求它是几条边 尚书坊

正多边形外角和公式是啥 搜狗搜索

多边形的角 禾教 初中数学互动课堂

09多边形的外角和平行四边形初中数学初二 Youtube

正多角形の内角と中心角 家紋の描き方007b 夏貸文庫