選択した画像 正の平方根をとる 266043-正の平方根を取る

累乗根 るいじょうこん root 方程式 x n ＝a（a は実数）を満足する x の値を，a の（正の）n 乗根といい，これを a 1/n と表す。 a の n 乗根の個数は，範囲を複素数にまで広げて考えれば一般に n 個ある。 a の n 乗根のうち実数値をとるものは，(1) a が正，n が偶数のとき ，(2) a が正，n が奇数の 25という数字は5を二乗したもの (5×5=25)ですよね？ ということは、"5"は、５を二乗した時の"25″に対するもとの数となります。 つまり、5は25の平方根であると言えるのです。 Excelで平方根を計算する方法は以下の3つがあります。お好みの方法をお使いください。 SQRT関数を使う方法 SQRT（スクエア・ルート）関数は、数値の正の平方根を返す関数です。SQRT関数を使ってExcelで平方根を計算する手順は以下の通りです。 作業時間：1分

電卓でルート 平方根 を計算する方法

正の平方根を取る

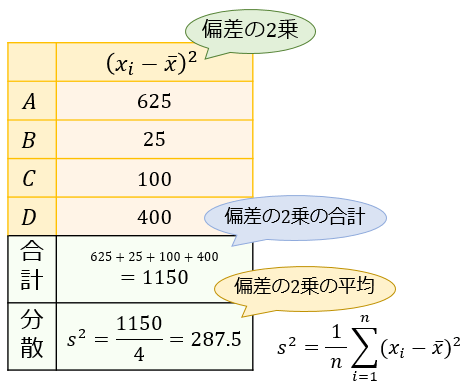
正の平方根を取る- 算出した偏差の二乗という指標の平均値をとる、これが分散です！ step4 分散の正の平方根をとる(toeicの例だと分散の単位が「点^2」となっている。「標準偏差は 点です」と単位揃えて議論したいため) これが分散・標準偏差の全貌です。1 4 平方根 平方根の計算 が真値よりも大きければ は負となるので、 の値が正となるまで (1 10) を繰り返せば良い。 さて、除算のときと同じように繰り返しの回数を検討しよう。 の場合は単純に平方根をとる

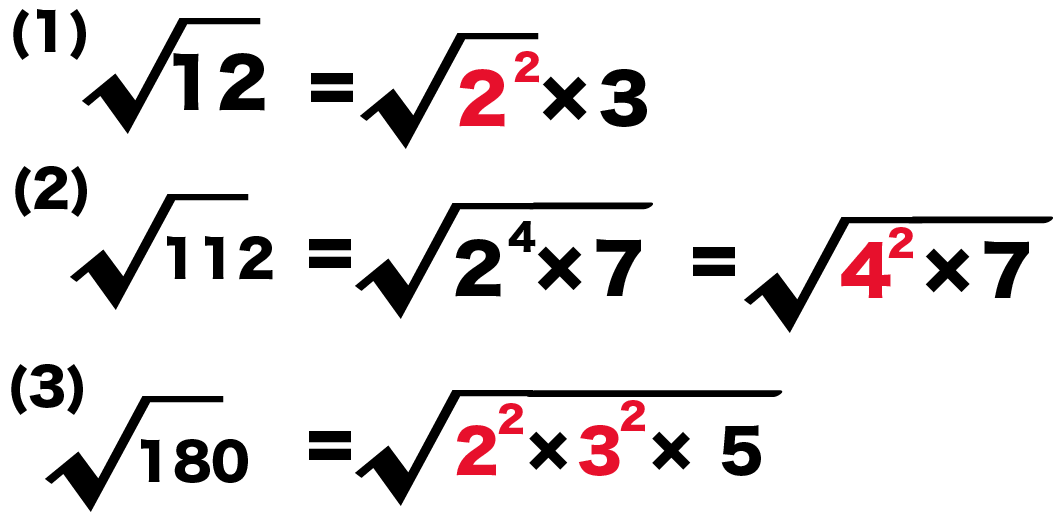
平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

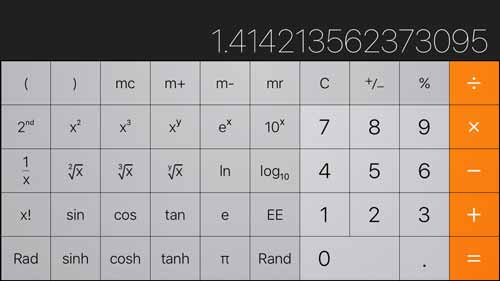
二次式の 根 の公式）は次の式で与えられる： 二次方程式 a x 2 b x c = 0 ( a ≠ 0 ) {\displaystyle ax^ {2}bxc=0\quad (a\neq 0)} の解は x = − b ± b 2 − 4 a c 2 a {\displaystyle x= {\frac {b\pm {\sqrt {b^ {2}4ac}}} {2a}}} 二次方程6 平方根を取る とはどういう 7 答えが2になる複雑な数式を探 8 －01と－001ってどっちが大き 9 xが分子の足し算、どうやるんで 10 絶対値の中に絶対値 11すると、入力した値の正の平方根の値が表示されます。写真では $\sqrt{2}$ の値 が表示されています。 正の平方根の値が表示された 以上が、iPhone にデフォルトで入っている電卓アプリでルートの計算をする方法です。

平方根の加減 3 ＋2 を例に考える。 まず をaとおくと、 3 ＋2 ＝3a＋2a＝5a ここでaに をもどすと、答えは5 になる。 したがって平方根の加減では、根号の中身は変えずに、根号の外側だけを計算する。 平方根は文字式と同様の考え方で計算できる。こうして平方根が求まる理由を考えると，次の桁を求める段階で次の計算をおこなってい ることがわかる．すなわち，xに対してy2 xとなるyまで求まっているとき，2yが左に， x−y2 が右に得られている．次の桁はzとしてもとめるが，それは(2yz)z x−y2 となる 出来るだけ大きなzになるよう1桁分平方根は、根号（ルート）を使って表すことができます。 ある正の数の平方根のうち、正の方を $\sqrt{a}$ と書き、「ルート a」と読みます。負の方は $\sqrt{a}$ となります。 それでは、もう一つ平方根を求める問題を解いてみましょう。

– SD = 標準偏差とは、分散を平方根にとることによって計算される値です。 – skew = 歪度とは、分布の非対称性を示す指標。値が正であると分布が右に伸びている。逆に負であると左に伸びている。C = 0 の場合 ところで、先ほどは根号の中の定数 C を正の実数に限定しましたが、それ以外では成り立たないのでしょうか。 例えば C = 0 の場合はどうなるでしょう。 先ほどと同じ方法で C = 0 の場合を考えると、 x^2 x = 0 となり、 x は0と1の二つが答えになってしまいます。一般に、a が正の数のとき、a の平方根のうち、正の方を 、負の方を と表します。 記号√を 根号 （こんごう）といいます。 a が0でないとき、平方根は正と負の2つありましたが、 3 {\displaystyle {\sqrt {3}}} は正の数だけを表すことに注意してください。

正の数 負の数 減法 トランプを引いてとるのと同じ Youtube

平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ

0 の平方根は 0 のみであり、平方根が一意に定まるのはこのときに限られる。 単位長と任意の長さ a が与えられたとき、 a の正の平方根の長さは定規とコンパスを用いて作図することができる。 定義 数 a に対して、 x 2 = a を満たす x を a の平方根という。Np var および np std で分散と標準偏差を求めることができる マセマ出版社の「初めから始める数学I」という参考書を使って勉強しているのですがその中で(ab)2√ab= (√a√b)^2この両辺は正で、√a√b > 0 よりこの両辺の正の平方根をとると√(ab)2√ab = √a√b↑この√は全体にかかっていますとな

素数判定のときに 平方根をとってそれ以下の素数で割り切れるか判定し Yahoo 知恵袋

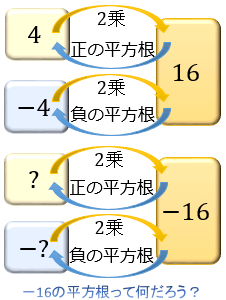
16は16の正の平方根というのが理解できません 教えてくだ Yahoo 知恵袋

 可逆行列 a に対して、ユニタリ行列 u および正定値行列 p が一意に存在して a = up と書ける。 これを a の極分解と呼ぶ。 この正定値行列 p は正定値行列 a*a の主平方根であり、 u は u = ap −1 で求まる。 a が可逆でないときでも、適当な方法で p が定まれば（それは一意であり）極分解解決方法が見つかりました！ ある意味ではこれは些細な質問ですが、別の場合、実際には非常に深いです！ 他は述べたように、平方根を取ることを意味同じ単位持つ。Stdev(X)Stdev⁡(X)\operatorname{Stdev}(X)XXX 平方根を取ることはあなたに与えられる絶対的な均質性別名絶対スケーラビリティを。正の実数の平方根を求める 実数 a > 0 に対して を作図する． (1)直線上の3点a, b, cをab = a, bc = 1 となるようにとる． (2)線分acの中点をdをとり，d中心の 半径adの円を描く． (3)bを通る線分acの垂線と上の円の交点を eとする． (4)!このときbe = ．

平方根 Wikipedia

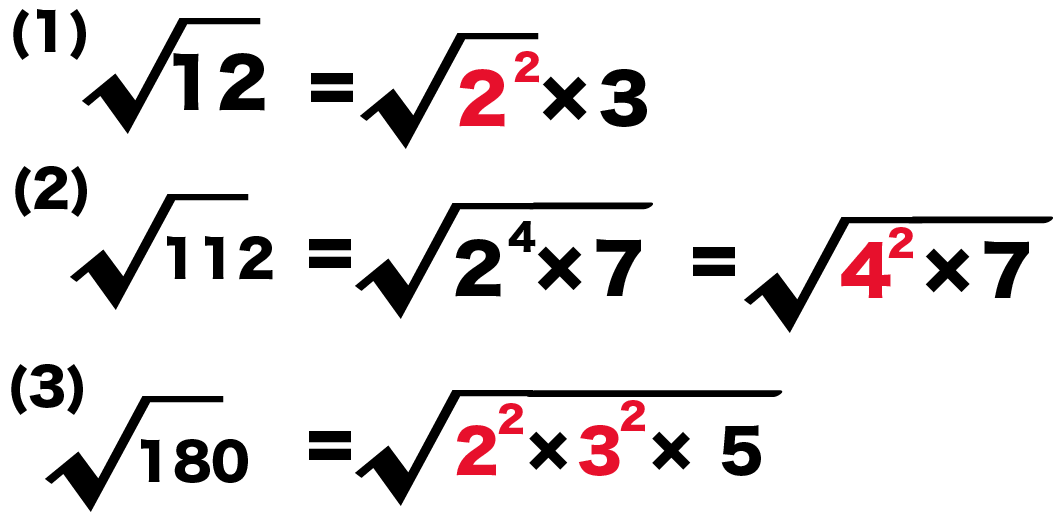
平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

 任意の正の実数 x > 0 について同様の議論が成立するため、任意の正の実数は正の平方根を持つことが明らかになりました。 一意性の証明正の実数 x > 0 に対して、異なる2つの正の平方根 y 1, y 2 > 0 が存在するものと仮定して矛盾を導きます。 仮定より したがって、ルートとは同じ数を2回かけたものの根(元となるもの)という意味です。 0の平方根は0のみであり、どんな正の数aに対しても平方根は正と負の2つ存在し、 そのうち正である方を√を使って と表します。 つまり、 である必要があるのです。1 単元名 平方根 2 単元について （1） 単元観 学習指導要領では、本単元において「正の数の平方根について理解し、それを用いて表現し考察する ことができるようにする」とある。具体的には「数の平方根の必要性と意味を理解すること」，「数の平

高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド

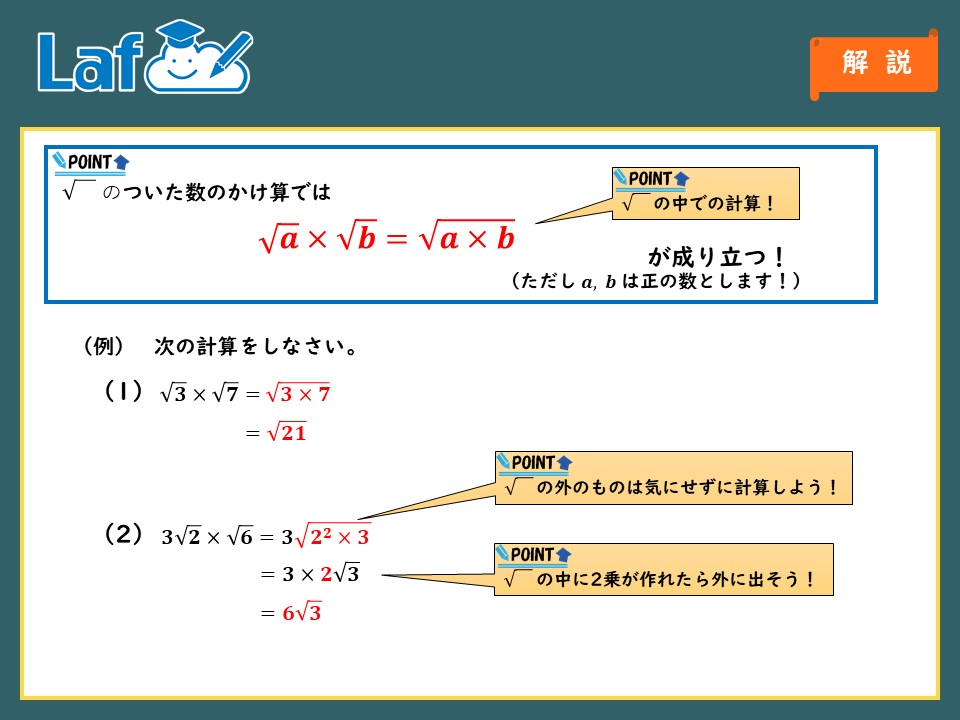
これで完璧 平方根の基礎 中3数学 中学生の勉強法

平方根についてまとめると，次のようになる。 00 正の数の平方根は ア 個ある。 この ア 個の数は イ が等しく， ウ が異なる。 000 の平方根は エ である。 ア ～ エ に当てはまる正しい組み合わせを，次の ～ から つ選び，その正の平方根をとるとA/ 3 が得られます． 図32 (a)正規分布の確率密度関数．m は平均．s は標 準偏差．(b)じゃんけんを3 回やったときの勝ち 数から負け数を引いた値の確率分布．両者はよ く似てい4．合成標準不確かさの計算（二乗和の平方根で合成） 合成標準不確かさuc を求めるには，各標準不確かさを二乗し，足し合わせ，その正の平方 根をとる。測定のモデル式をY f X1, X2,XN とし，出力量Y の推定値つまり測定の結果 n

2

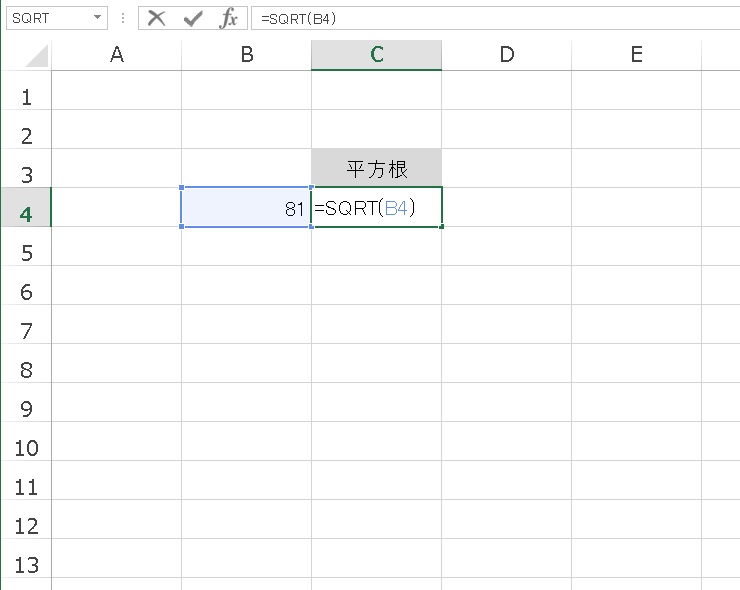
エクセルで平方根 ルート を求めるsqrt 関数 統計学が わかった

 両辺が正のとき,両辺を平方でき 4 3のn1乗はどうやって解けばよ 5;正の平方根の作図 o を通り ox に垂直な直線をひき，oe' = 1，oa' = a となる点 e'，a' を o に対して反対側にとる。平方根 √ 、立方根 3√ 、累乗根 n√ を計算します。

Excel Sqrtで平方根 ルート を計算する

平方根の問題です 大小を不等号で表す問題なんですが 3分の1は 3分の1より小さ Clear

 両辺が正であることも、 √a√b>0であることも、正の平方根をとる事がどういうことかも分かっているのですが 両辺が正で√a√b>0なら、なぜ両辺の正の平方根をとることになるのかがわかりません。 よろしくお願いします。実際に、 二次方程式の解の公式 （ 英 Quadratic formula;25の平方根は5と−5 の2つですが，そのうちの負の方を で表します． だから， です． 正の数 a に対して， a の平方根をまとめて で表し，プラス・マイナス・ルート a といいます． 例9 9の平方根は すなわち です． 例10 25の平方根は すなわち です．

平方根 ルート の計算

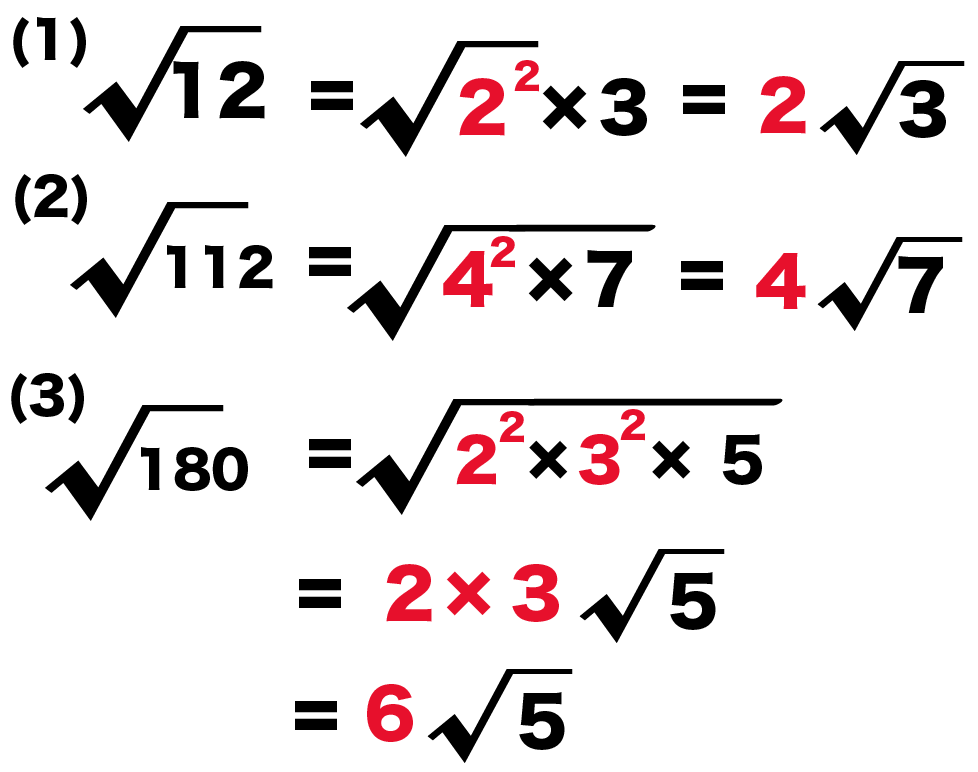
平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

 簡単公式正四角錐の表面積の求め方がわかる3つのステップ 中3数学 中学数学相似の証明問題の書き方がわかる3ステップ 中3数学 平方根・ルート分数の分母の有理化のやり方がわかる3つのステップ 38 個の行列の平方根とは？ 主平方根をとる 固有値が正の実数となる他の任意の平方根 t は t = i m の形で m が冪零かつ n と（したがって l と）可換となるようにとれる。しかしこのとき 0 = s 平方根とは 平方根とはなんでしょう？ 例えば3や3を2乗すると9になります。 このときの3や3を9の平方根といいます。 つまり2乗するとある数になる数を平方根というってことです。 そんなに難しくなさそうですね。 それでは例題をしてみましょう

7の平方根は 7ですよね また 49 7これは 7の平方根が Yahoo 知恵袋

２の話 その３７ キーを何度も押すとなぜ１になるの その１ かかしさんの窓

 今度は cos θ の時点ではやくも平方根筆算を使う羽目になった。ここから周長を求めるので、もう1回平方根をとる。 あれ？ 正24角形のときは 313 だったのに、正48角形にすると 312 となり、本来の値から遠ざかってしまった。円に近づくはずなのに。数 a が与えられたとき、二乗（平方）して a となる数、つまり、 x2 ＝ a となる数 x を a の平方根という。 a が正の数のときは、 a の平方根は正の数、負の数それぞれ一つずつあり、その絶対値は等し4 平方根の作図 7 5 放物線の性質 9 6 与えられた1点を通る放物線の接線と2次方程式 11 8 角の三等分再論 16 9 正多角形を折る 21 なる点a′ をとる

平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

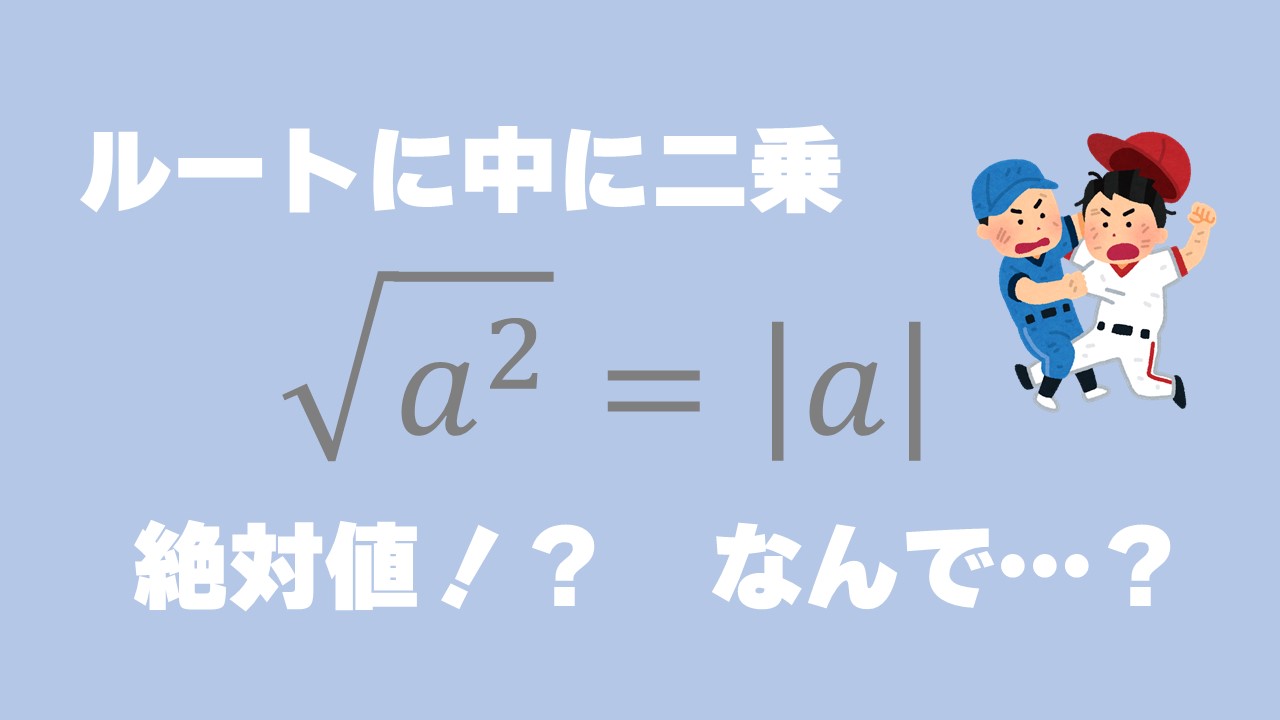
ルートの中身が絶対値に なんで場合分けが必要なのか 数スタ

 数であることが重要であった。それから，実際に自己同型で不変になる式( )2 の平方根 をとることと，解と係数の関係 により対称性を崩した。ここで今一度，高等学校数学ii正の平方根は05乗なので、Excelのセルに『=数値^05』と入力して計算できます。 また、Excelの関数の『=sqrt(数値)』を使うこともできます。 43 自由度修正決定係数〈補正R2〉 ：説明変数の数を考慮した当てはまりの指標

中学校数学 3年生 数量 平方根 Wikibooks

1

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

平方根 へいほうこん の意味 Goo国語辞書

平方根 ルート64 8 ではない の意味がわかりません 中学数学 定期テスト対策サイト

平方根の定義と基本的な公式 思考力を鍛える数学

中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ

電流公式覚え方 電力 電圧 電流の関係と計算方法を解説 簡単な覚え Mtlpe

平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ

標準偏差をエクセルで求める方法と完璧なグラフの作り方 Udemy メディア

円周率の定義は 大人が間違える子供の算数 Nikkei Style

宇宙を歩く高校数学 基礎

平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

1

これで完璧 平方根の基礎 中3数学 中学生の勉強法

これで完璧 平方根の基礎 中3数学 中学生の勉強法

電卓でルート 平方根 を計算する方法

標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ

2

平方根とは ヘイホウコンとは 単語記事 ニコニコ大百科

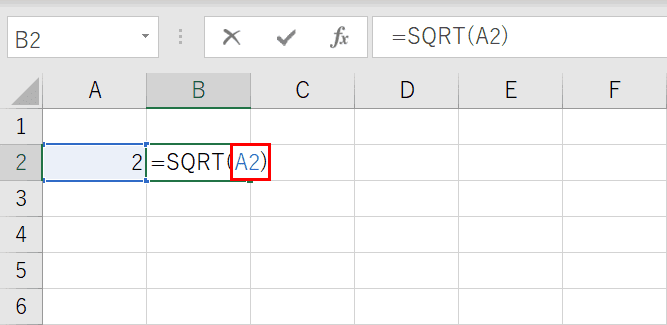
エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack

3

エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ

平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ

Excel関数 平方根 ルート を求める Sqrt関数

中学校数学 3年生 数量 平方根 Wikibooks

1

平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典

エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack

平方根 ルート の重要な計算方法まとめ 数学fun

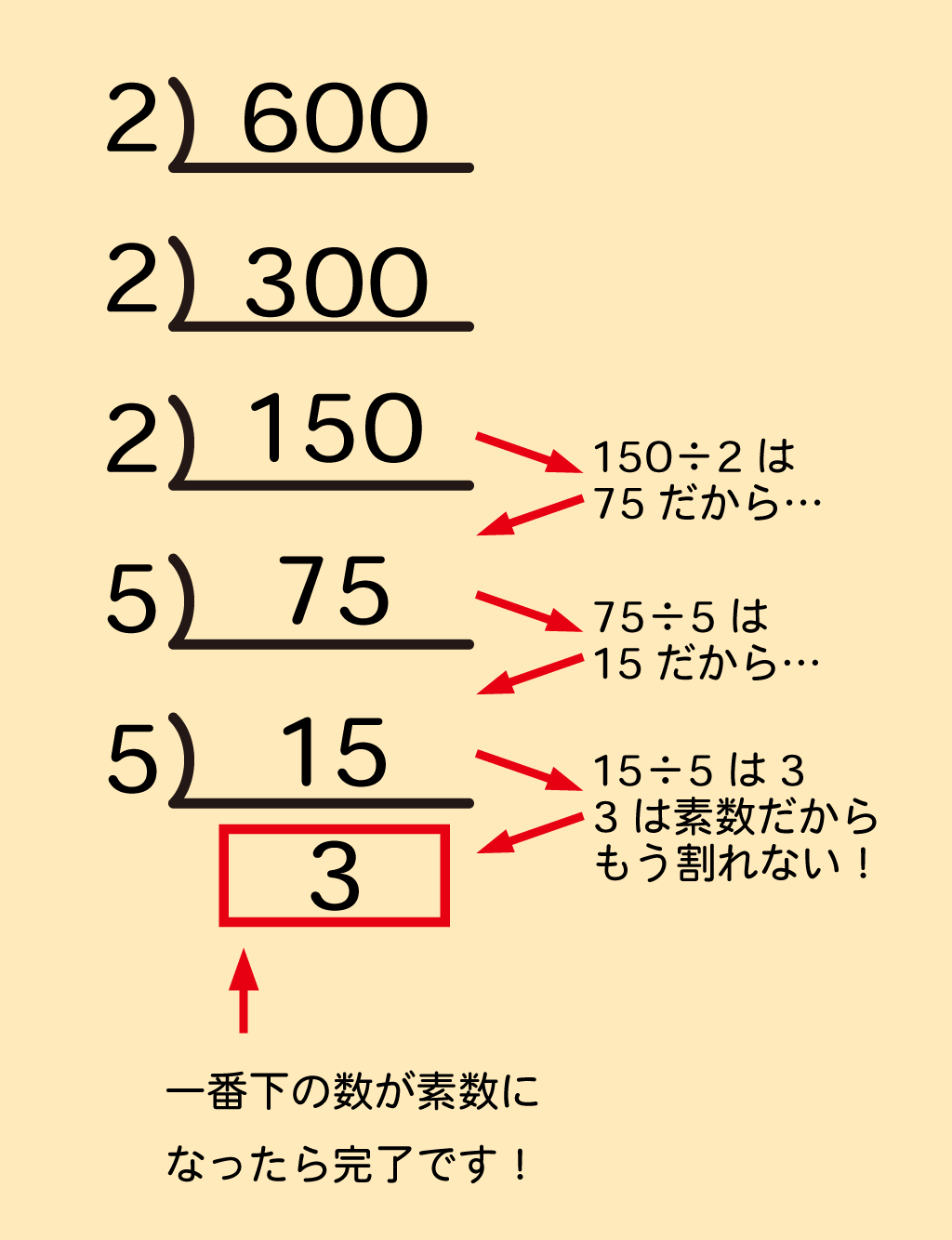
中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ

センター数 A 追第1問 大学受験in北海道

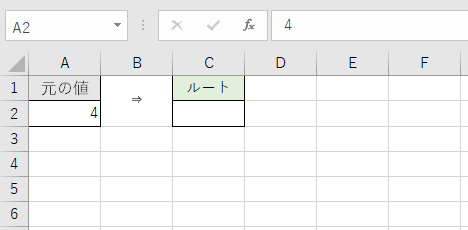
画像あり エクセルの関数を使ってルート 平方根 を計算 表示するには 基本と応用 ワカルニ

平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

これで完璧 平方根の基礎 中3数学 中学生の勉強法

平方根の利用 1 整数 自然数になるようなn 標 難 数学の解説と練習問題

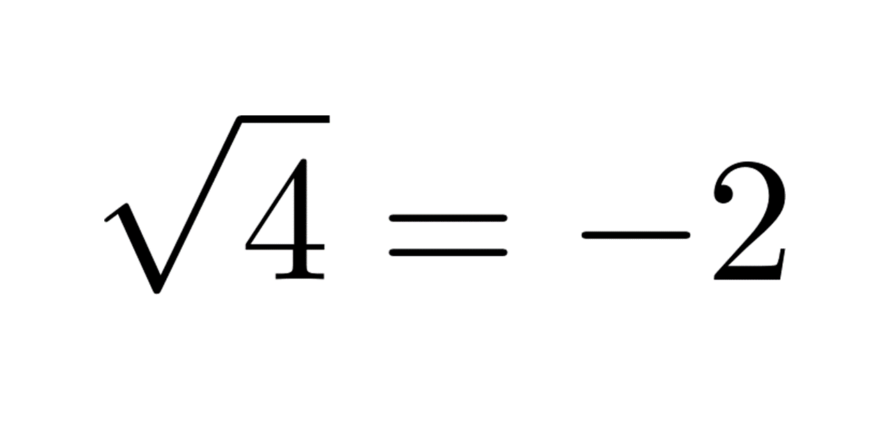
Sqrt 4 2 を実感する 多価関数への誘い 数学 統計教室の和から株式会社

中3数学 ルート 根号 の外し方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく

正の平方根を求めるアルゴリズム Qiita

標準偏差とは ビジネスでの活用方法と求め方を解説 リサーチコラム Gmoリサーチ

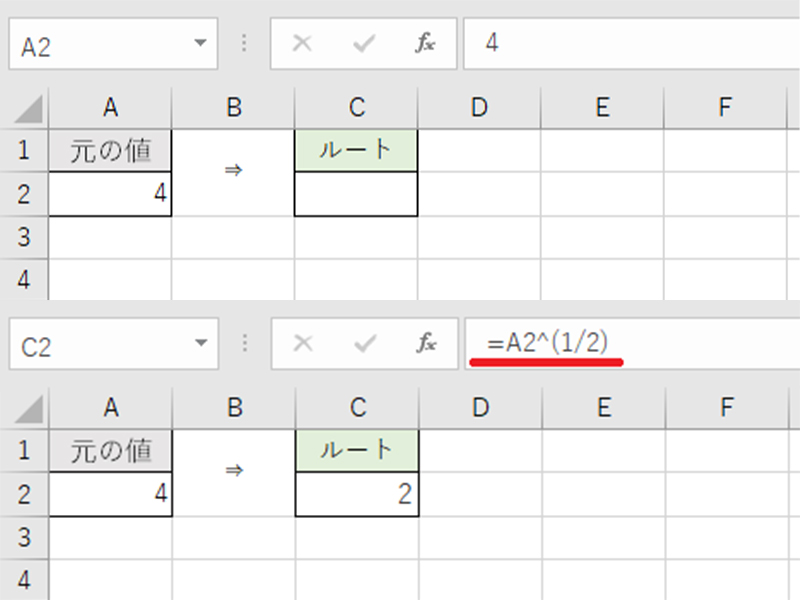
画像あり エクセルの関数を使ってルート 平方根 を計算 表示するには 基本と応用 ワカルニ

平均 分散 標準偏差 ｶﾜｲｲ裏番長のｃ言語がスキちゃん

2

北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む

6 2 標準偏差 統計学の時間 統計web

と 3 5はどちらが大きいですか 比べ方を教えてくださ Yahoo 知恵袋

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

数学ia 絶対値と平方根の計算を解こう Himokuri

平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

両辺の二乗をとる の逆ってなんていうんですか つまり 両辺にルートをつけたい Yahoo 知恵袋

相関係数 R とは 公式と求め方 相関の強さの目安を解説 受験辞典

実数 平方根とルート 平方根とルートの基本を理解しておこうの巻 Vol 4 ３回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校

ワークの答えに 2aは二乗すると2aの二乗になるから 2aの二乗の正の平方根 Yahoo 知恵袋

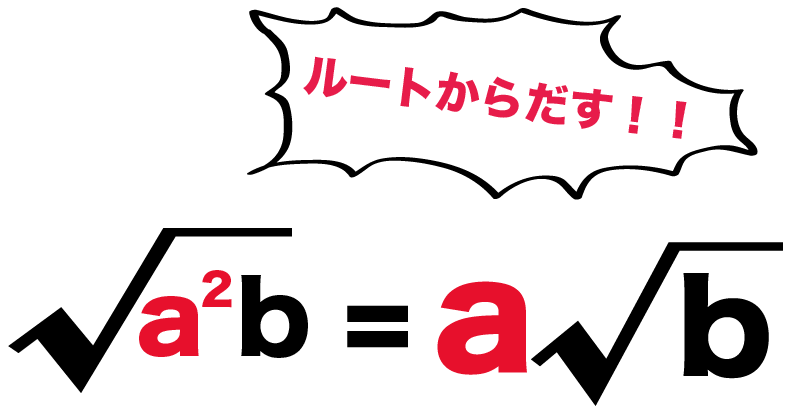
平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

顧問p モテ偏差値の計算式 50 自分のモテ得点 モテ平均点 モテ標準偏差 10 まず個々のモテ得点を算出してそれをモテ平均点から引いて二乗して平均をとってモテ分散を出す モテ分散の正の平方根がモテ標準偏差 調べるなら母数たくさん欲しいな

２の話 その３７ キーを何度も押すとなぜ１になるの その１ かかしさんの窓

教師の統計学 標準偏差を求める意味は なぜ分散の正の平方根なのか 高校教師とictのブログ 数学 情報 Ict

中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ

平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス

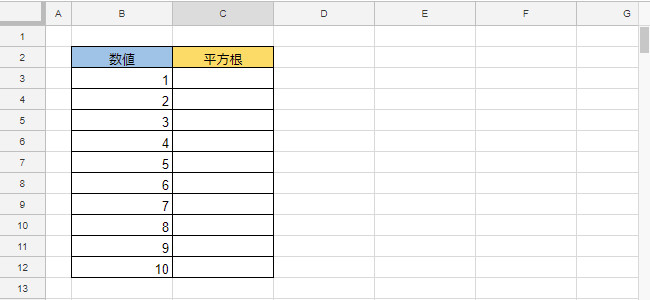
Sqrt 正の平方根を求める スプレッドシート関数

Fdkyb3b9c093sr81e Com E8 A3 E6 9e 90 E5 Ad A6 E8 87 E7 B4 A0 E6 95 B0 81 Ae E8 A8 E7 Ae 97

平方根 ルート の重要な計算方法まとめ 数学fun

中学校数学 3年生 数量 平方根 Wikibooks

６ なぜ は正の方だけ表すのか 数学史による考察 アクチュアリー試験数学の研究

実数は二乗して負にならないということに質問です Clear

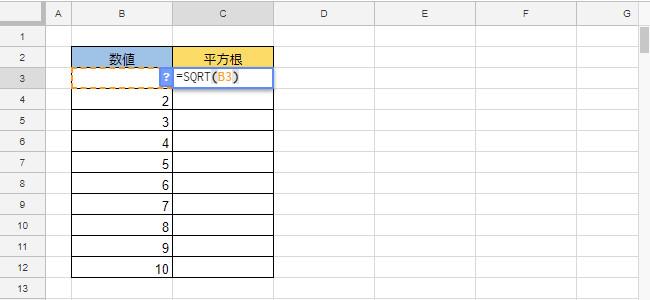
Sqrt 正の平方根を求める スプレッドシート関数

中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ

平方根とルートの違い ルート外しの注意点 趣味の大学数学

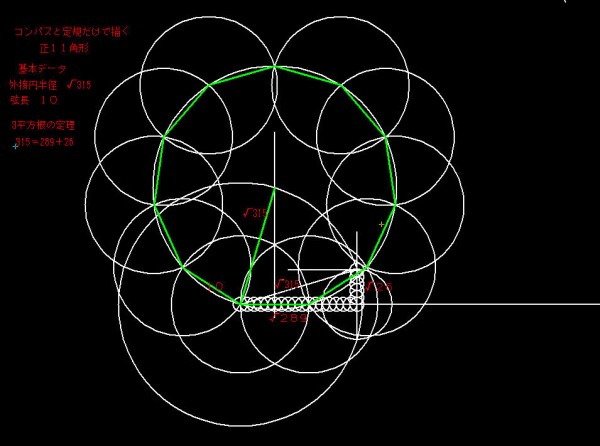
定規とコンパスだけで描く 正１１角形の描き方 公開 発想力教育研究所 素数誕生のメカニズム

化学平衡定数の問題です 線を引いてあるところの 負符号は捨て Yahoo 知恵袋

２の話 その３７ キーを何度も押すとなぜ１になるの その１ かかしさんの窓

中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会

1枚目教えていただけませんか ちなみに課題1の左ってのが2枚目 Clear

中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ

平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典

ルート9って3じゃないですかルートaの二乗って絶対値aじゃないですかだから答えがa Clear

Fatali 暴走ルーン仕様変更について 数字好きとして言わせてもらうと A Bの絶対値の差を試行数で割ってるから 上振れも下振れも数字を拾ってしまう以上おかしな数値出るのは当たり前 正と負で とるか 絶対値の二乗の和の平方根をとらないとダメよ

2乗してルートをつけると絶対値 数学の偏差値を上げて合格を目指す

高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド

平方根とは コトバンク

２乗 平方根

2乗して10になる数 はどう求める じつは分数でも書けます 横山 明日希 ブルーバックス 講談社 1 3

正の平方根ってなんですか 笑 よく分からないです 教えてくれる方いたら嬉しいです Clear

平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ

Incoming Term: 正の平方根を取る,