√無料でダウンロード！ 三平方の定理 円 2つ 578225-三平方の定理 円 2つ

三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し例 (1) 1 2 x 斜辺がxなので 1222=x2 x2 = 5 x > 0 より x= 5 (2) x 12 13 斜辺が13なので x2122 三平方の定理とは、次のような定理です。 三平方の定理（ピタゴラスの定理） 上のような直角三角形で、次の等式が成り立つ。 a2 b2 = c2 a 2 b 2 = c 2 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきました

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

三平方の定理 円 2つ

三平方の定理 円 2つ-円と三平方 弦の長さ 円の中心から弦に垂線を引くと、弦の垂直二等分線になる。 例 半径7の円で、中心から弦abまでの距離が3である。 弦abの長さを求める。 やり方 ab=xとする。 直角三角形apoで、ap= x 2 、ao=7、po=3を 三平方の定理にあてはめる。 (x 2) 2 三平方の定理を使えば、2点間の距離は3ステップで計算できるよ。 次の例題を一緒に考えてみよう。 2点A (1,5), B (2,1)の間の距離を求めてください。 Step1 図をかく まずは座標と点を図にしてみて。 練習問題でも図をかいてみようか。 2点の座標をポチッ

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

 ここで三平方の定理を使うのです。 すると この式にさっきのh=5、r=√3を代入すると よって a=2√7 という答えが出ました。 三平方の定理の逆とは 三平方の定理の逆とは、3辺の長さがa、b、cである三角形において、 a²b²=c²三平方の定理 三平方の定理(1) 1 次の図でxの値を求めなさい。 374 3㎝ 4㎝ 三平方の定理より x ＝4 ＋3 ＝16＋9 ＝ x ＞0だから x ＝ 答え x 2 2 2 2 次の図でxの値を求めなさい。 3 次の長方形の対角線の長さを求めなさい。 対角線の長さをx ㎝とすると 三平方の定理より、 それで、三平方の定理を使えば、 2× 2 ＝√3×√3＋ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度、 60 度、 30 度になる このことは三平方の定理

三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 これですね。 2辺が直角 (すなわち90°)となるように接し、その2辺の端を円の基本的な性質 弦、接線、接点という言葉は覚えていますか？ その図形的性質は覚えていますか？ 覚えていないとまったく問題が解けませんので、必ず暗記しましょう。 弦と二等辺三角形 円 \(o\) とパソコンで知る高校数学 「三平方の定理」をめぐる証明について 4444 10．．．．面積を2通りに計算して比較する その3 内接円を用いて面積を計算 ン直角三角形の場合は3辺の長さから 内接円半径を簡単に求めることができる。

三平方の定理5 (3)解説 を組み合わせた図形である。 影をつけた部分の面積を求めよ。 図のようにEからBに直線を引いて2つの部分に分け、それぞれの部分の面積を出す。 (i) まず青色の部分の面積を出す。 また、EとBは中心をCとする円周上の点なのでEC=6cm直角三角形OAPで三平方の定理を用いる。 A P O 5cm 10cm x OA=5cm (半径), OP=10cm, AP=xcm x252=102 x2=75三平方の定理を用います。 \(AB^2=3^26^2\) \(AB^2=45\) \(AB \gt 0\) なので \(AB=\sqrt{45}\) \(AB=3\sqrt{5}\) 次のページ 三平方の定理・直方体の対角線の長さ;

Mathematics 三平方の定理 ４ 円と三平方の定理 働きアリ The 2nd

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

18 三平方の定理(2) ～三平方の定理の利用～ ホップ ステップ ジャンプ 19 円 (1) ～円周角の定理～ ホップ ステップ ジャンプ 円 (2) ～円周角の定理，円周角の定理の逆～ ホップ ステップ ジャンプ 21 円 (3) ～円と直線～ ホップ方べきの定理(2) 定理 点pを通る2直線の一方が円oと 2 点 a，b で交わり，もう一方が点 t で接するとき pa∙pb lpt 6 下の図で，pt は接線，t は接点である。𝑥 を求めよ。 (1) (2) (1) 方べきの定理により 5∙ 5 e4 ;回転図形2 円と三平方の定理 *** よく出る応用 *** 三角形2個の問題1 三角形2個の問題2 三角形2個の問題3 特別な形の三角形1 特別な形の三角形2

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるのかずお式中学数学ノート14 中3 円の性質・三平方の定理 著者の高橋一雄先生が「かずお式中学数学ノート14」（朝日学生新聞社刊）をテキストにして、ビデオ講義をしています。 内容は式の計算を扱っています。 テキストさえ購入していただければ、何度三平方の定理は の定理ともいう。 三平方の定理 答 2， 2， 2，ピタゴラス ＝ ＝ ＝ ＝ 問1 次の直角三角形で， の値を求めなさい。 ① ② ③ ④ BCを分けて 考えたらいいね cm 8 5 6 3

3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4

4 三平方の定理 問題① 下図の二等辺三角形abcの面積を求めよう。 5 三平方の定理 問題② 下図で、apは pを接点とする 円oの接線である。円oの半径を 6cm、線分oa の長さを12とするとき、線分apの長さを求めよう。直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので，次の図で AH=DC になる． この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり， HC三平方の定理三平方の定理と円21解答 2 = 7 2 − 2 = 45 0

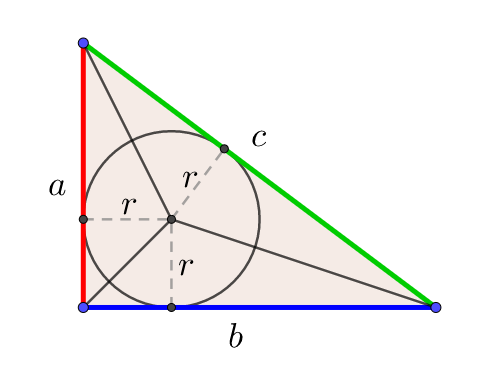
三平方の定理の証明４ 直角三角形と内接円 キソカラ

三平方の定理を利用するのはわかったんですけど 三平方の利用の仕方とそのあとがわかりま Clear

/ 三平方の定理の逆 / 有名角と比 / 2点間の距離 / 円の中心と弦との距離 / 空間図形の対角線・高さ / 空間図形とひもの最短距離 円の性質 中3数学で学ぶ「円の性質」のテストによく出るポイントと問題を三平方の定理 三平方の定理と円11 無料で使える中学学習プリント 三平方の定理 xls Created Date 2/8/17 PM三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と

中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座

 方べきの定理とその統一的な証明 方べきの定理とは，円と点 P P P と2本の直線が作る図形において， P A 1 × P A 2 = P B 1 × P B 2 PA_1\times PA_2=PB_1\times PB_2 P A 1 × P A 2 = P B 1 × P B 2 が成立するという定理です。方べきの定理は全部で3パターンあります。三平方の定理（ピタゴラスの定理） 三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という三平方の定理を直接証明するというものではないので、ややこしく感じるかもしれません。 納得できない人のために、次は図で直感的に理解できるよう解説します。 三平方の定理が直感的にわかる図 三平方の定理は各辺の2乗の等式です。

三平方の定理 覚えておきたい基本公式を解説 数スタ

三平方の定理を直角三角形二つで証明 Youtube

円の方程式はピタゴラスの定理で求められます。また円の中心が原点から離れた場合の方程式は「(x－a) 2 (y－b) 2 =r 2 」です。今回は円の方程式の意味、公式、半径との関係について説明します。ピタゴラスの定理、半径の詳細は下記が参考になりますL𝑥 6 𝑥 645 𝑥0 より 𝑥3√5

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

1

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三平方の定理

数学 中3 61 三平方の定理 基本編 Youtube

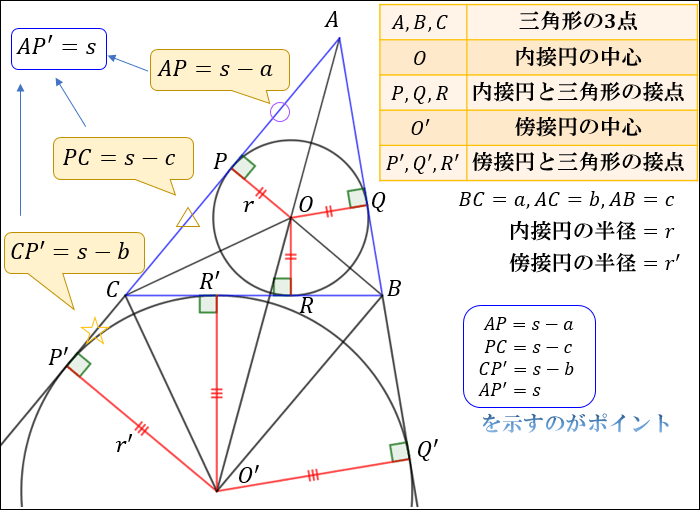
ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月

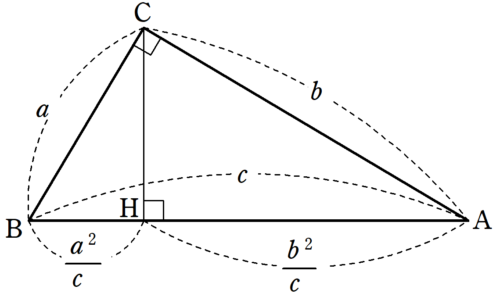
三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ

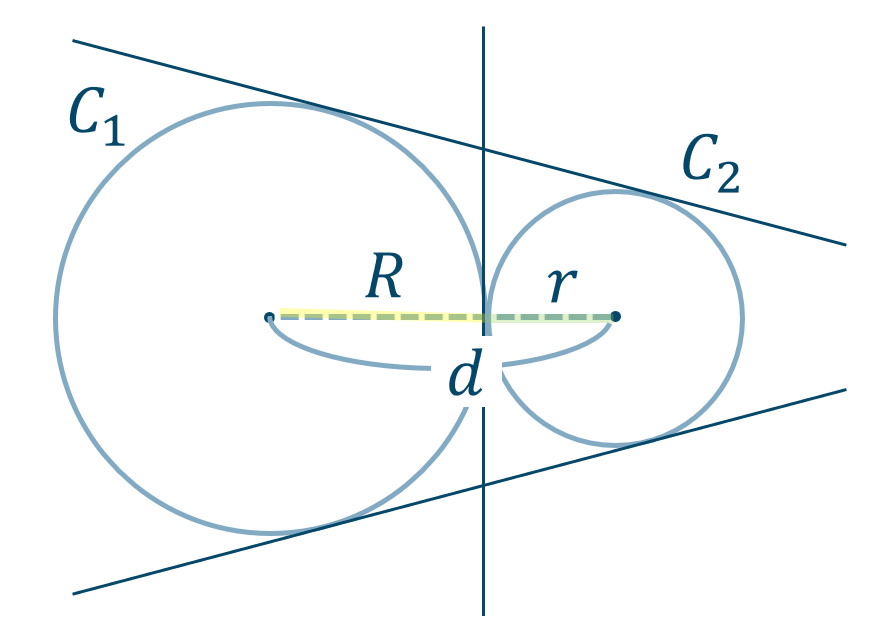
公式一覧と使い方 解き方 数学ａ 図形の性質 教科書より詳しい高校数学

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

ม 3 โน ตของ 中3数学 三平方の定理の利用 ช น Junior Clear

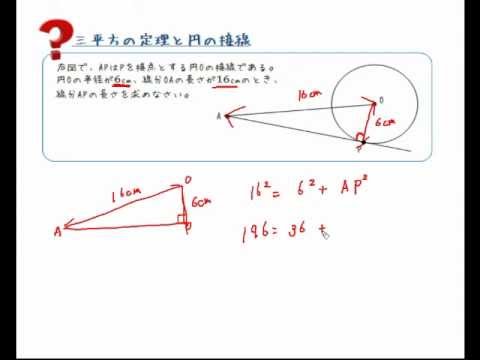
三平方の定理と円の接線 Youtube

三平方の定理の問題です 下の図で 直線abは2つの円o O の共通な接 Okwave

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

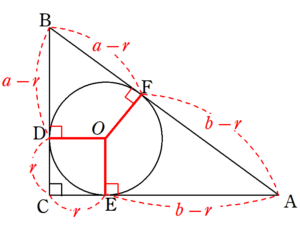
三平方の定理の証明 内接円の利用 Fukusukeの数学めも

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

1

1999 号 三平方の定理用教材 Astamuse

三平方の定理の証明と使い方

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

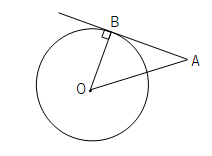
中3数学 三平方の定理の定期テスト対策問題 Examee

Math 三角形に内接する円 働きアリ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

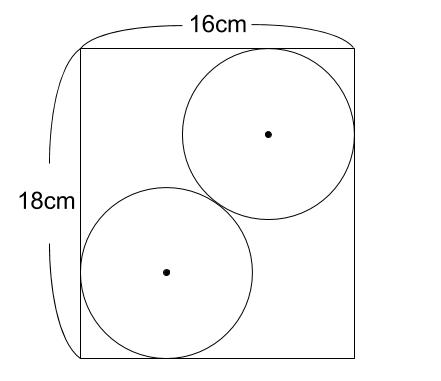
長方形に内接する2つの円 中学数学の無料オンライン学習サイトchu Su

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

数学a 平面図形 円の性質 ２つの円の共通接線

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Math 高校入試の難問 円と接線 働きアリ

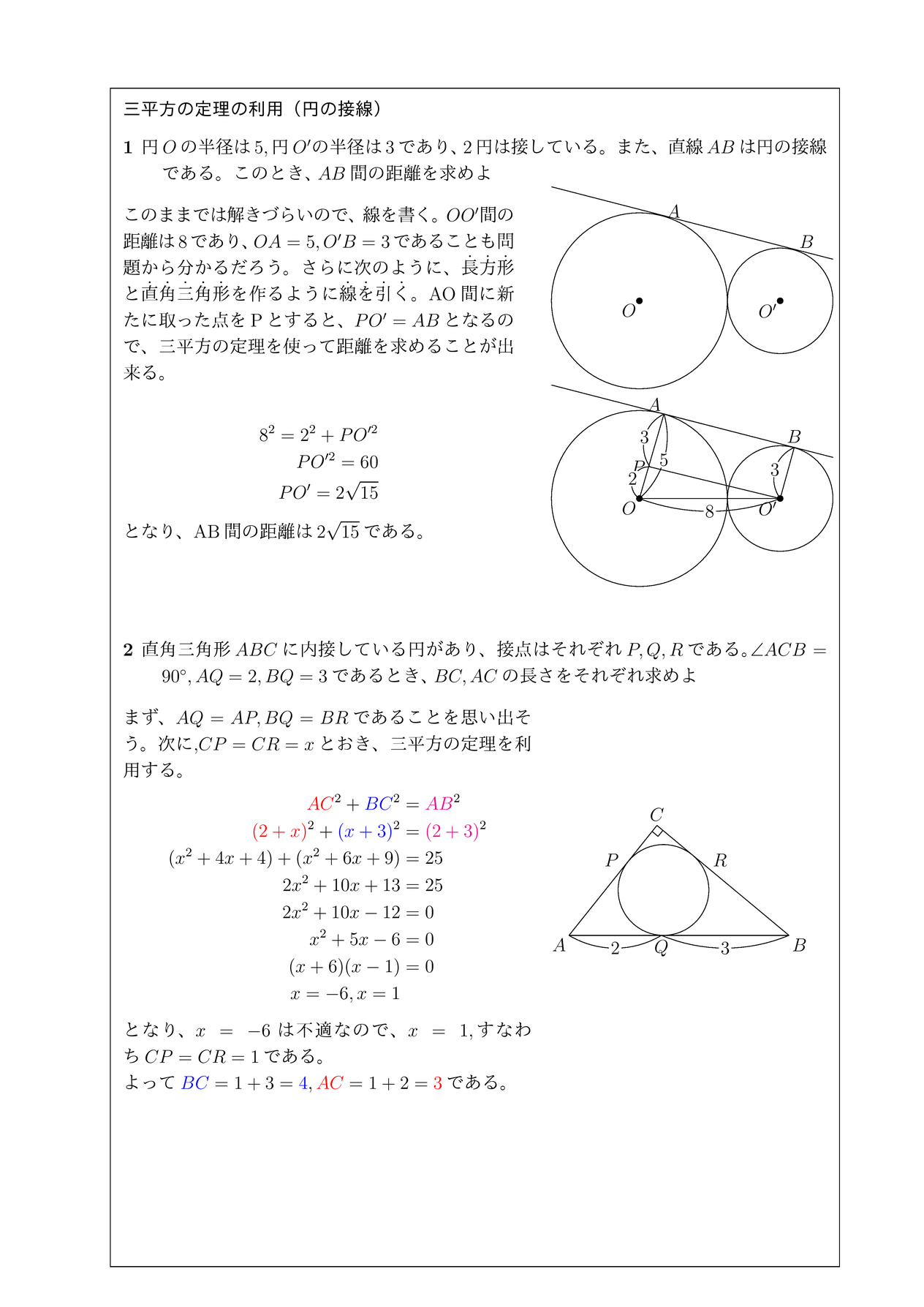
三平方の定理の利用 円の接線 チーム エン

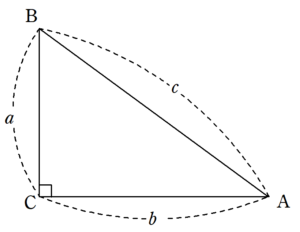
三平方の定理の証明 内接円の利用 Fukusukeの数学めも

質問コーナー Discuss Scratch

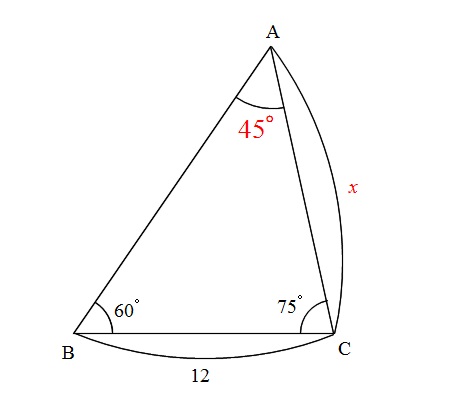
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

三平方の定理と円 さわってうごく数学 Aquaアクア For Android Apk Download

三平方の定理から円周率を計算してみる Yamav1 02bのブログ

余弦定理 は三平方の定理の進化版 余弦定理は2つある

高校数学a 共通接線の長さを求める問題 例題編 映像授業のtry It トライイット

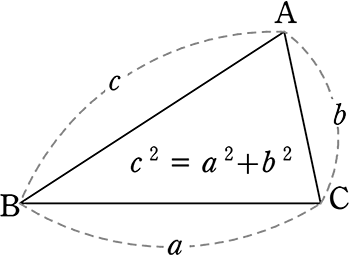
中学数学 三平方の定理

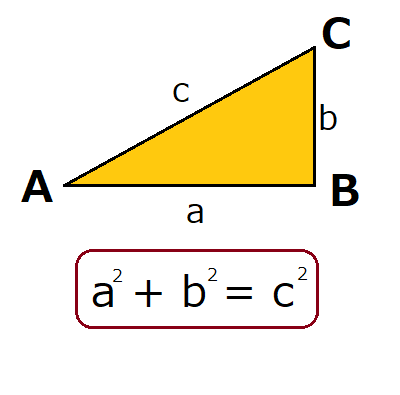
三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

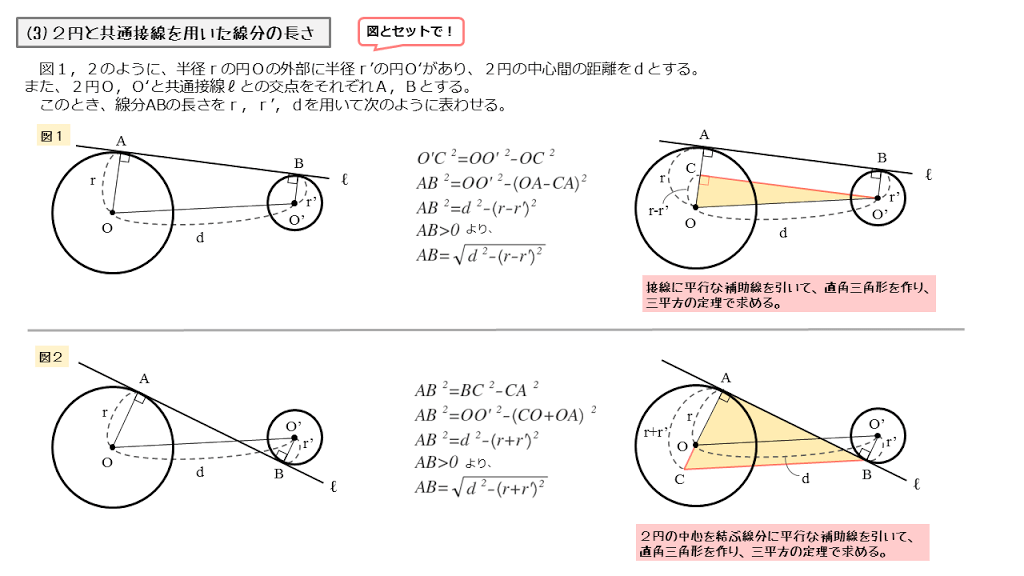
図形の性質 ２円の位置関係について 日々是鍛錬 ひびこれたんれん

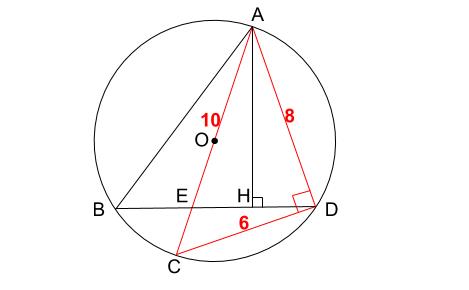
高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su

Mathematics 三平方の定理 ４ 円と三平方の定理 働きアリ The 2nd

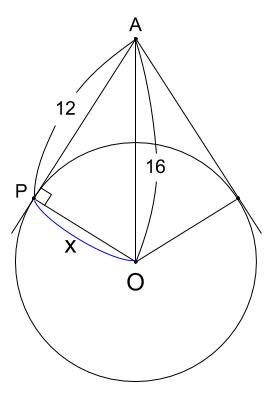
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

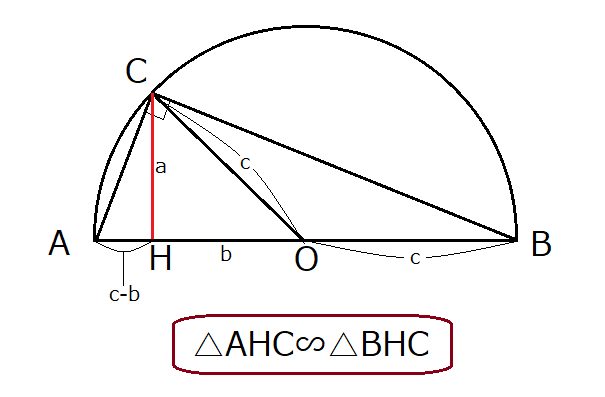
三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋

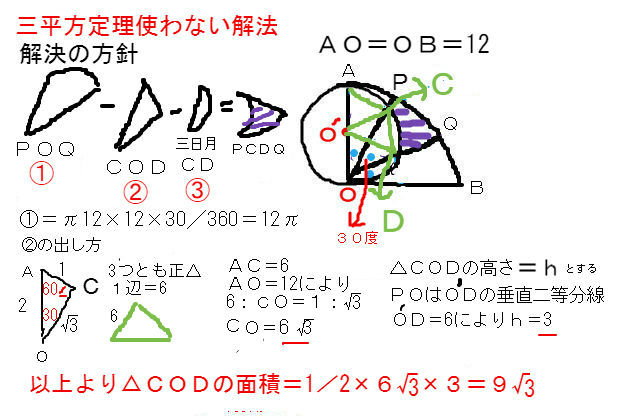
複雑求績問題 三平方定理使わずに解く方法 中学数学 理科 寺子屋塾の復習サイト

2つの円の位置関係と共通接線の求め方 図形と方程式 2

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

1

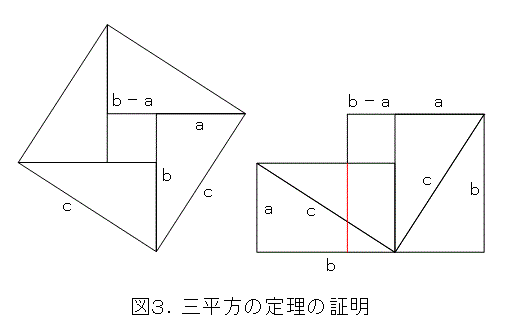
三平方の定理の拡張について考えよう 理科好き子供の広場

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

3 つの直角三角形の内接円 思考力を鍛える数学

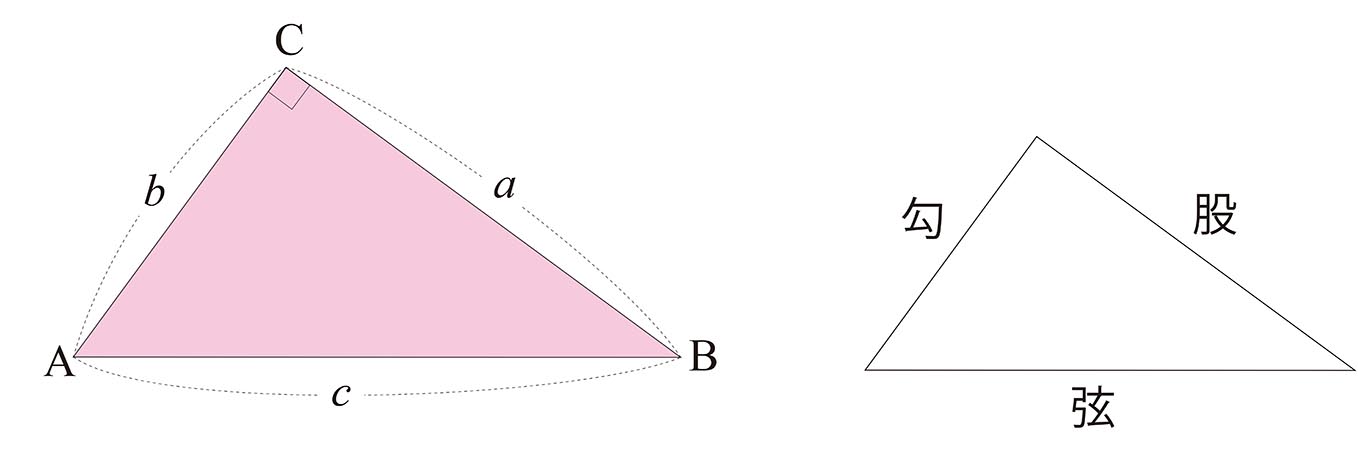
コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション

正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理の証明４ 直角三角形と内接円 キソカラ

三平方の定理の証明と使い方

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

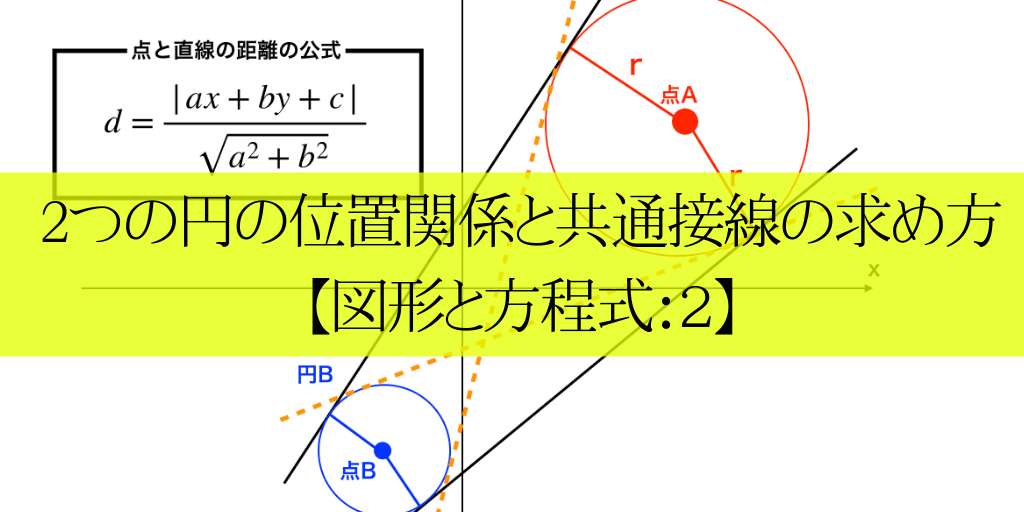
2つの円の位置関係と共通接線の求め方 図形と方程式 2

三平方の定理です どっちかでもよいので Xの値の求め方教えてください Clear

三角形の中に接する半径の等しい2つの円 中学校の幾何の問題ですが 数学 教えて Goo

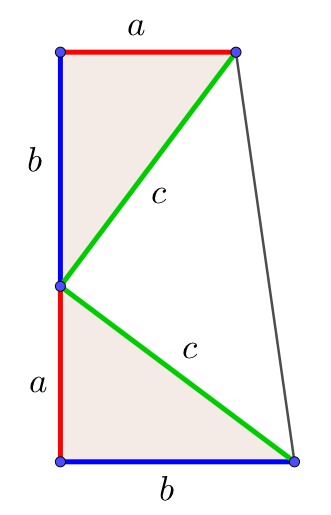
三平方の定理の証明３ 大統領の台形 キソカラ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

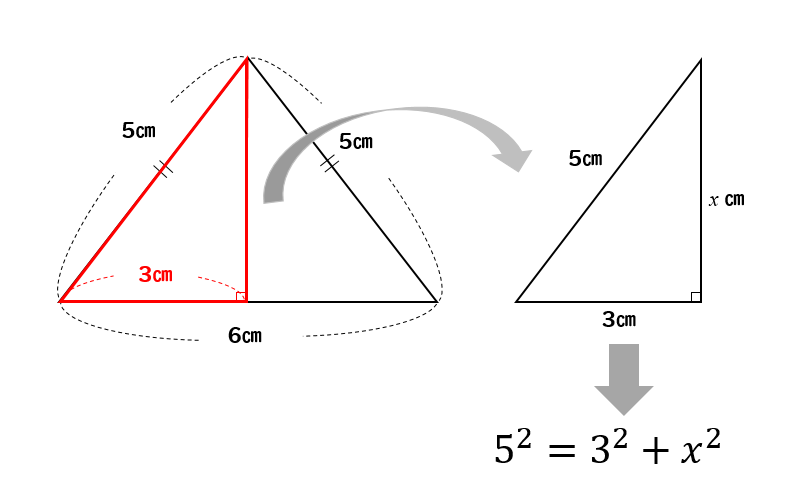
高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

円 接線 三平方の定理 三角形の面積 知能問題 数的処理 判断推理 数的推理 数学パズル ｓｐｉ 空間把握 解いてみてください

三平方の定理の証明と使い方

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

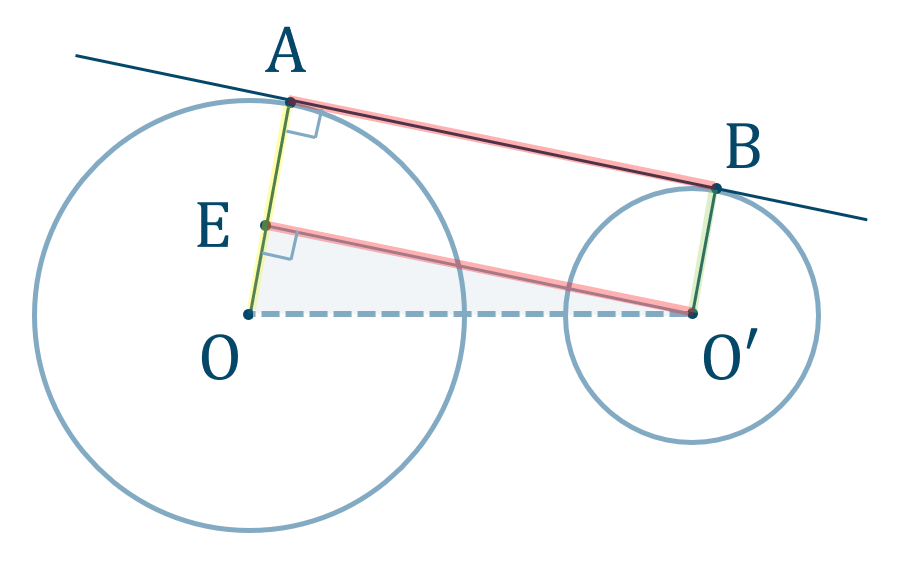
公式一覧と使い方 解き方 数学ａ 図形の性質 教科書より詳しい高校数学

1999 号 三平方の定理用教材 Astamuse

三平方の定理の４通りの美しい証明 高校数学の美しい物語

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理 応用 内接円 Youtube

高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月

三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ

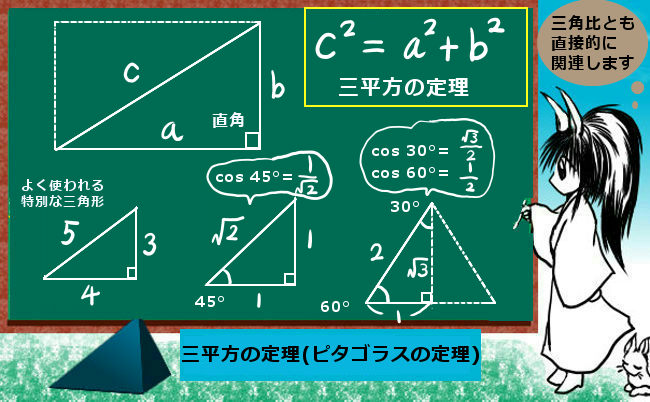
三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori

中3の数学の問題 セルモ大蔵 世田谷 の塾長ブログ

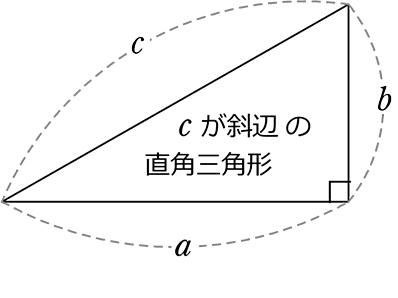
中学数学 三平方の定理

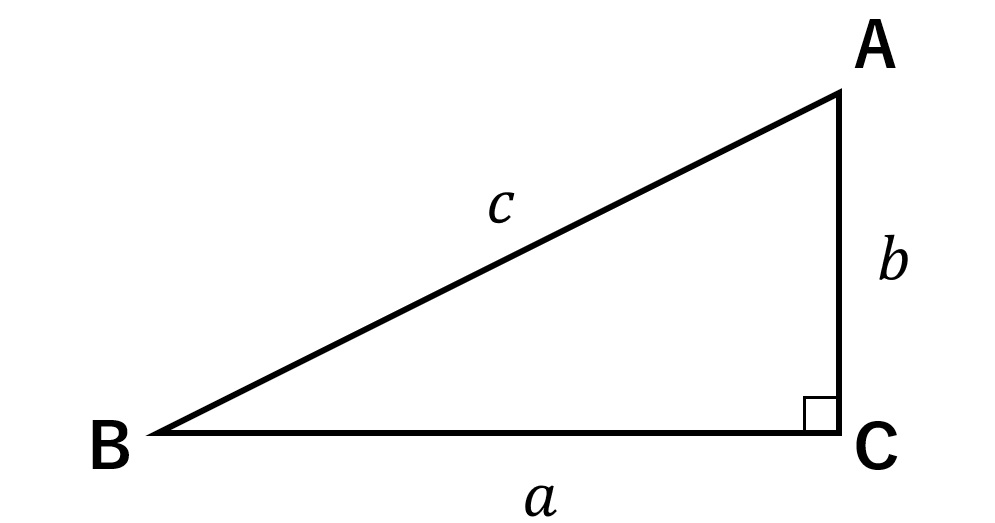
感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

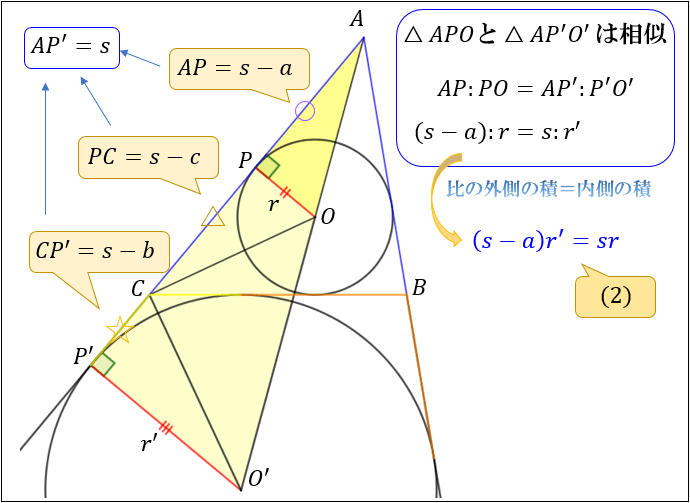
ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

三平方の定理の証明 直感的に分かる図で解説します 数学fun

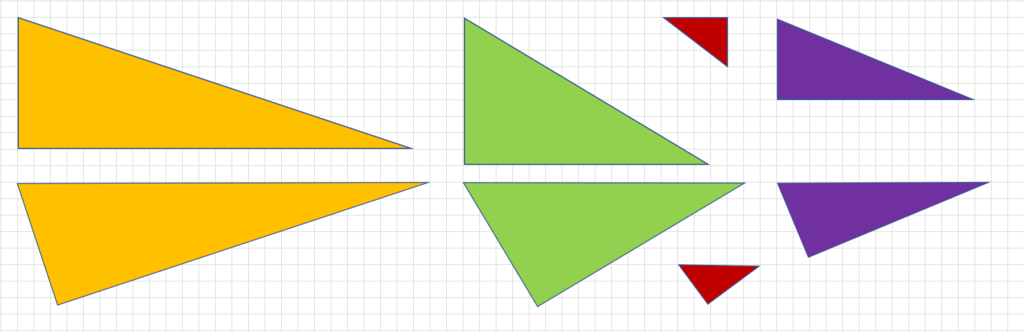
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

Incoming Term: 三平方の定理 円 2つ,